题目内容
一宇宙飞船以v=1.0×104 m/s的速度进入密度为ρ=2.0×10-9kg/m3的微陨石流中,如果飞船垂直于运动方向上的最大截面积为S="5" m2,且认为微陨石与飞船碰撞后都附着在飞船上,则飞船受到的平均制动力多大?
1.0 N
此类问题在正确地建立起“物理模型”后,关键是找出动量发生变化的那部分质量与时间的关系,即找出在某一Δt时间内动量变化的那部分质量Δm.由于连续体问题,无法用牛顿运动定律求解,可以建立一物理模型用动量定理求解.
建立如下的“管道模型”:在时间△t内被飞船吸附的陨石都分布在以S为横截面积、长为L=v·Δt的柱体内,这部分微小陨石的质量Δm=ρSL=ρvSΔt.它们被吸附后具有的动量p2=Δm=ρv2SΔt,吸附前的动量为p1=0.
根据动量定理得飞船作用于这些陨石的平均作用力大小为F=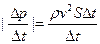 =ρv2S
=ρv2S
根据牛顿第三定律,飞船受到的平均制动力的大小为:F′=F=ρv2S=2.0×10-9×(1.0×104)×5 N="1.0" N.
建立如下的“管道模型”:在时间△t内被飞船吸附的陨石都分布在以S为横截面积、长为L=v·Δt的柱体内,这部分微小陨石的质量Δm=ρSL=ρvSΔt.它们被吸附后具有的动量p2=Δm=ρv2SΔt,吸附前的动量为p1=0.
根据动量定理得飞船作用于这些陨石的平均作用力大小为F=
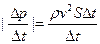 =ρv2S
=ρv2S根据牛顿第三定律,飞船受到的平均制动力的大小为:F′=F=ρv2S=2.0×10-9×(1.0×104)×5 N="1.0" N.

练习册系列答案
相关题目

 ="0.5" m的细线系住,在光滑水平面上做匀速圆周运动,线速度大小v="2" m/s,则从图示A点运动到B点(T/2)细线拉力的冲量为多少?
="0.5" m的细线系住,在光滑水平面上做匀速圆周运动,线速度大小v="2" m/s,则从图示A点运动到B点(T/2)细线拉力的冲量为多少?