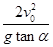题目内容
如图所示,O为竖直平面内圆周的最高点,A、B、C、D为圆周上的四点,现让小物块沿OA、OB、OC、OD由静止下滑,下滑到A、B、C、D四点所用的时间分别为tA、tB、tC、tD.不计摩擦,则( )

| A.tD>tC>tB>tA | B.tA=tB=tC=tD |
| C.tA>tB>tC>tD | D.无法确定 |

设小物块下滑的轨道与竖直方向的夹角为θ,根据牛顿第二定律得,a=
=gcosθ.轨道的位移x=2Rcosθ.
根据2Rcosθ=
at2
解得t=
,与θ角无关.所以tA=tB=tC=tD.故B正确,A、C、D错误.
故选B.
| mgcosθ |
| m |
根据2Rcosθ=
| 1 |
| 2 |
解得t=
|
故选B.

练习册系列答案
相关题目
 如图所示,B为竖直圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一小球在圆轨道左侧的A点以速度v0平抛,恰好沿B点的切线方向进入圆轨道.已知重力加速度为g,则AB之间的水平距离为( )
如图所示,B为竖直圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一小球在圆轨道左侧的A点以速度v0平抛,恰好沿B点的切线方向进入圆轨道.已知重力加速度为g,则AB之间的水平距离为( )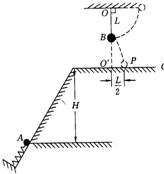 如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L,小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生碰撞,碰撞中无机械能损失,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P点的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L,小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生碰撞,碰撞中无机械能损失,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P点的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:


 B.
B.
 D.
D.