题目内容
(I)某同学在实验室用如图所示的装置来研究牛顿第二定律.

(1)如图甲,①调整长木板倾斜时时沙桶是否要悬挂?答
②小车质量M、沙和沙桶的总质量m的关系是
(2)在此实验中,该同学先接通打点计时器的电源,再放开纸带,如图乙是在m=100g,M=1kg情况下打出的一条纸带,O为起点,A、B、C为过程中的三个相邻的计数点,相邻的计数点之间有四个点没有标出,有关数据如图乙,则小车的加速度为
(3)不断改变沙和沙桶的总质量m,测出对应的加速度a,则下列图象中能正确反映小车加速度a与质量m的关系的是


(1)如图甲,①调整长木板倾斜时时沙桶是否要悬挂?答
否
否
.正确的调整应是小车拉着纸带作匀速直线运动
拉着纸带作匀速直线运动
②小车质量M、沙和沙桶的总质量m的关系是
M>>m
M>>m
,在此条件下可以认为绳对小车的拉力近似等于沙和沙桶的总重力,在控制小车的质量不变的情况下,可以探究加速度与合力的关系.(2)在此实验中,该同学先接通打点计时器的电源,再放开纸带,如图乙是在m=100g,M=1kg情况下打出的一条纸带,O为起点,A、B、C为过程中的三个相邻的计数点,相邻的计数点之间有四个点没有标出,有关数据如图乙,则小车的加速度为
0.95
0.95
m/s2.(3)不断改变沙和沙桶的总质量m,测出对应的加速度a,则下列图象中能正确反映小车加速度a与质量m的关系的是
C
C

分析:(1)①调整长木板倾斜时沙桶不能悬挂;正确的调整应是:在不悬挂沙筒时,给小车一个初速度,小车能够带动纸带匀速下滑.
②设砂和砂桶的总质量为m,小车的质量为M,则小车在运动过程中根据牛顿第二定律得M与M之间的关系;
(2)由于在A于B之间和B与C之间还有4个点没有标出,所以两个计数点之间的时间间隔是T=5t,根据导出公式:△x=aT2即可计算出小车的加速度;
(3)正确的a-F图象应该是过原点的直线,由于不断改变沙和沙桶的总质量m,因此图象会发生弯曲.
②设砂和砂桶的总质量为m,小车的质量为M,则小车在运动过程中根据牛顿第二定律得M与M之间的关系;
(2)由于在A于B之间和B与C之间还有4个点没有标出,所以两个计数点之间的时间间隔是T=5t,根据导出公式:△x=aT2即可计算出小车的加速度;
(3)正确的a-F图象应该是过原点的直线,由于不断改变沙和沙桶的总质量m,因此图象会发生弯曲.
解答:解:(1)①调整长木板倾斜时沙桶不能悬挂;正确的调整应是:在不悬挂沙筒时,给小车一个初速度,小车能够带动纸带匀速下滑.
②设砂和砂桶的总质量为m,小车的质量为M,则小车在运动过程中根据牛顿第二定律得:
对于小车:F=Ma
对于砂和砂桶:mg-F=ma;
解得:F=
=
;
所以满足m<<M的条件下,小车在运动过程中受到的合外力近似等于砂和砂桶的总重力,能减小该实验的系统误差.
(2)由于在A于B之间和B与C之间还有4个点没有标出,所以两个计数点之间的时间间隔是T=5t,根据导出公式:△x=aT2得:
a=
=
=
×10-2m/s2=0.95m/s2;
(3)由(1)的方向知,F=
=
,根据牛顿第二定律得:a=
=
当m的质量较大时,a-m的图线将向下弯曲.故图C正确.
故答案为:(1)①否 小车拉着纸带作匀速直线运动②M>>m(2)0.95 (3)C.
②设砂和砂桶的总质量为m,小车的质量为M,则小车在运动过程中根据牛顿第二定律得:
对于小车:F=Ma
对于砂和砂桶:mg-F=ma;
解得:F=
| Mmg |
| m+M |
| mg | ||
1+
|
所以满足m<<M的条件下,小车在运动过程中受到的合外力近似等于砂和砂桶的总重力,能减小该实验的系统误差.
(2)由于在A于B之间和B与C之间还有4个点没有标出,所以两个计数点之间的时间间隔是T=5t,根据导出公式:△x=aT2得:
a=
| △x |
| T2 |
| ||||
| T2 |
| 62.00-42.05 |
| (5×0.02)2 |
(3)由(1)的方向知,F=
| Mmg |
| m+M |
| mg | ||
1+
|
| F |
| M |
| mg |
| m+M |
故答案为:(1)①否 小车拉着纸带作匀速直线运动②M>>m(2)0.95 (3)C.
点评:在“验证牛顿第二定律”的实验用控制变量法,本实验只有在满足平衡摩擦力和小车质量远大于钩码质量的双重条件下,才能用钩码重力代替小车所受的合力,同时加强基础物理知识在实验中的应用,加强解决实验问题的能力.

练习册系列答案
相关题目

 某同学在实验室中找到一只小灯泡,标称功率值为0.75W,额定电压值已模糊不清,为了得到额定电压值,他先用欧姆表直接测出该灯泡的电阻约2Ω,然后根据公式计算出该灯泡的额定电压U=
某同学在实验室中找到一只小灯泡,标称功率值为0.75W,额定电压值已模糊不清,为了得到额定电压值,他先用欧姆表直接测出该灯泡的电阻约2Ω,然后根据公式计算出该灯泡的额定电压U=
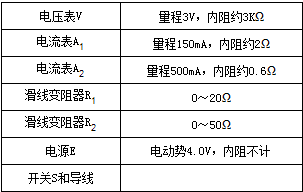
 (2011?信阳二模)某同学在实验室测定一节电池电动势和内阻,实验室中有如下器材:
(2011?信阳二模)某同学在实验室测定一节电池电动势和内阻,实验室中有如下器材: (2006?松江区二模)某同学在实验室先后完成下面二个实验:
(2006?松江区二模)某同学在实验室先后完成下面二个实验: