题目内容
8. 如图(a)所示为磁悬浮列车模型,质量M=1kg的绝缘板底座静止在动摩擦因数μ1=0.1的粗糙水平地面上.位于磁场中的正方形金属框ABCD为动力源,其质量m=1kg,边长为1m,电阻为 $\frac{1}{16}$Ω.与绝缘板间的动摩擦因数μ2=0.4,OO′为AD、BC的中线.在金属框内有可随金属框同步移动的磁场,OO′CD区域
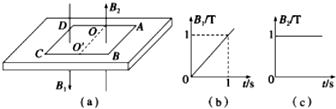
如图(a)所示为磁悬浮列车模型,质量M=1kg的绝缘板底座静止在动摩擦因数μ1=0.1的粗糙水平地面上.位于磁场中的正方形金属框ABCD为动力源,其质量m=1kg,边长为1m,电阻为 $\frac{1}{16}$Ω.与绝缘板间的动摩擦因数μ2=0.4,OO′为AD、BC的中线.在金属框内有可随金属框同步移动的磁场,OO′CD区域内磁场如图(b)所示,CD恰在磁场边缘以外;OO′BA区域内磁场如图(c)所示,AB恰在磁场边缘以内(g=10m/s2).若绝缘板足够长且认为绝缘板与地面间最大静摩擦力等于滑动摩擦力.
(1)若金属框固定在绝缘板上,则金属框从静止释放后,其整体加速度为多少?
(2)若金属框不固定,金属框的加速度又为多少?此时绝缘板是否静止,若不静止,其加速度又是多少?
分析 面积O′OAB内磁通量发生变化,回路中有感应电流产生,由此可以求出回路中电流的大小,线框受安培力和摩擦力作用,由此可以求出线框的加速度大小以及安培力的大小.
解答 解:(1)若金属框固定在绝缘板上,由题意得:
E=$\frac{△B1}{△t}$•$\frac{1}{2}$SABCD=1×$\frac{1}{2}$×1×1 V=0.5 V,
则电流为:I=$\frac{E}{R}$=8 A,
那么安培力为:FAB=B2IL=8 N,
取绝缘板和金属框整体进行受力分析,由牛顿第二定律有:
FAB-μ1(M+m)g=(M+m)a,
解得:a=3 m/s2.
(2)若金属框不固定,对金属框进行受力分析,假设其相对绝缘板滑动,有:
Ff1=μ2mg=0.4×1×10 N=4 N,
对金属框应用牛顿第二定律得:FAB-Ff1=ma1,a1=4 m/s2;
对绝缘板应用牛顿第二定律得:Ff1-Ff2=Ma2,Ff2=μ1(M+m)g=2 N,
解得:a2=2 m/s2,
a1>a2,假设正确.
金属框、绝缘板的加速度分别为4 m/s2、2 m/s2.
答:(1)若金属框固定在绝缘板上,则金属框从静止释放后,其整体加速度为3 m/s2.
(2)若金属框不固定,金属框的加速度又为4 m/s2此时绝缘板不静止,其加速度又是2 m/s2
点评 本题考查了有关电磁感应的电流、力、运动分析,涉及知识点较多,是考查学生综合应用知识能力的好题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
8.在物理学中,下列物理量中是矢量的是( )
| A. | 功率 | B. | 电流 | C. | 电势 | D. | 加速度 |
9.下列说法正确的是( )
| A. | 伽利略巧妙地运用科学的推理和实验验证,证明了物体在斜面上从静止开始运动时速度与时间成正比 | |
| B. | 亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快 | |
| C. | 物体处于静止或匀速直线运动时所受合力均为零 | |
| D. | 物体的质量越大,惯性越大 | |
| E. | 如果物体的运动速度只是方向发生了改变,则它的运动状态就没有改变 |
3.矿产资源是人类赖以生存和发展的物质基础,随着对资源的过度开采,地球资源逐步枯竭,已然使我们的环境恶化,而宇航事业的发展为我们开辟了太空采矿的途径.太空中进行开采项目,必须建立“太空加油站”. 假设“太空加油站”正在地球赤道平面内的圆周轨道上运行,其离地球表面的高度为同步卫星离地球表面高度的十分之一,且运行方向与地球自转方向一致.下列说法正确的有( )
| A. | “太空加油站”运行的加速度等于其所在高度处的重力加速度 | |
| B. | “太空加油站”运行的速度等于同步卫星运行速度的$\sqrt{10}$倍 | |
| C. | 站在地球赤道上的人观察到它向东运动 | |
| D. | 在“太空加油站”工作的宇航员因不受重力而在舱中悬浮或静止 |
13.下面关于速度和加速度关系的说法中正确的是( )
| A. | 速度变化越快加速度就越大 | B. | B速度减小时,加速度也一定减小 | ||
| C. | 速度为零,加速度也一定为零 | D. | 加速度增大时,速度也一定增大 |
20. 如图所示,纵坐标表示两个分子间引力、斥力的大小,横坐标表示两个分子间的距离,图中两条曲线分别表示两分子间引力、斥力的大小随分子间距离的变化关系,e为两曲线的交点,则下列说法正确的是( )
如图所示,纵坐标表示两个分子间引力、斥力的大小,横坐标表示两个分子间的距离,图中两条曲线分别表示两分子间引力、斥力的大小随分子间距离的变化关系,e为两曲线的交点,则下列说法正确的是( )
 如图所示,纵坐标表示两个分子间引力、斥力的大小,横坐标表示两个分子间的距离,图中两条曲线分别表示两分子间引力、斥力的大小随分子间距离的变化关系,e为两曲线的交点,则下列说法正确的是( )
如图所示,纵坐标表示两个分子间引力、斥力的大小,横坐标表示两个分子间的距离,图中两条曲线分别表示两分子间引力、斥力的大小随分子间距离的变化关系,e为两曲线的交点,则下列说法正确的是( )| A. | ab为斥力曲线,cd为引力曲线,e点横坐标的数量级为10-10m | |
| B. | ab为引力曲线,cd为斥力曲线,e点横坐标的数量级为10-10m | |
| C. | 由分子动理论可知:温度相同的氢气和氧气,分子平均动能相同 | |
| D. | 若两个分子间距离增大,则分子势能也增大 |
 如图所示,一货车车箱在外力的作用下以a=7.5m/s2的恒定加速度从静止开始沿水平面运动,当车厢开始运动的同时在车厢顶部中间位置有一个可视为质点的小球开始做自由落体运动.已知车厢质量为M=1×105kg,车厢高h=3.2m,g=10m/s2.求:
如图所示,一货车车箱在外力的作用下以a=7.5m/s2的恒定加速度从静止开始沿水平面运动,当车厢开始运动的同时在车厢顶部中间位置有一个可视为质点的小球开始做自由落体运动.已知车厢质量为M=1×105kg,车厢高h=3.2m,g=10m/s2.求: 在做“探究平抛运动”的实验时,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹.
在做“探究平抛运动”的实验时,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹.