题目内容
3.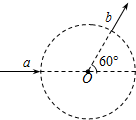 如图所示,磁感应强度为B的匀强磁场垂直纸面分布在半径为R的圆内,一带电粒子沿半径方向从a点射入,从b点射出,速度方向改变了60°;若保持入射速度不变,而使磁感应强度变为$\sqrt{3}$B,则粒子飞出场区时速度方向改变的角度为( )
如图所示,磁感应强度为B的匀强磁场垂直纸面分布在半径为R的圆内,一带电粒子沿半径方向从a点射入,从b点射出,速度方向改变了60°;若保持入射速度不变,而使磁感应强度变为$\sqrt{3}$B,则粒子飞出场区时速度方向改变的角度为( )| A. | 90° | B. | 45° | C. | 30° | D. | 60° |
分析 带电粒子进入磁场中做匀速圆周运动,由牛顿第二定律可得到轨迹半径表达式,分析出磁感应强度变为$\sqrt{3}$B时轨迹半径与原来轨迹半径的关系,结合轨迹求解.
解答  解:带电粒子进入磁场中做匀速圆周运动,由 qvB=m$\frac{{v}^{2}}{r}$,得:r=$\frac{mv}{qB}$
解:带电粒子进入磁场中做匀速圆周运动,由 qvB=m$\frac{{v}^{2}}{r}$,得:r=$\frac{mv}{qB}$
当磁感应强度由B变为$\sqrt{3}$B时,轨迹半径变为原来的$\frac{\sqrt{3}}{3}$r,即:r′=$\frac{\sqrt{3}}{3}$r.
设粒子原来速度的偏向角为α,B变化后速度的偏向角为β.根据几何关系有:
tan$\frac{α}{2}$=$\frac{R}{r}$,
tan$\frac{β}{2}$=$\frac{R}{r′}$
又 α=60°
则得:β=90°
所以粒子飞出场区时速度方向改变的角度为90°.
故选:A.
点评 带电粒子在匀强磁场中匀速圆周运动问题,关键是画出粒子圆周的轨迹,往往用数学知识求轨迹半径与磁场半径的关系

练习册系列答案
相关题目
13.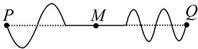 一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )
一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )
 一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )
一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示,对于其后绳上各点的振动情况,以下判断正确的是( )| A. | 两列波将同时到达中点M | |
| B. | 两列波波速之比为1:2 | |
| C. | 中点M的振动总是加强的 | |
| D. | M点的位移大小在某时刻可能为零 | |
| E. | 绳的两端点P、Q开始振动的方向相同 |
14.关于万有引力定律的表达式F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下面说法中正确的是( )
| A. | 公式中G为引力常量,它是由实验测得的 | |
| B. | 当r趋近于零时,万有引力趋近于无穷大 | |
| C. | m1与m2相互的引力总是大小相等,方向相反,是一对平衡力 | |
| D. | m1与m2相互的引力总是大小相等,方向相反,是相互作用力 |
18.下列说法中与物理学史实相符的是( )
| A. | 牛顿认为力是改变物体运动状态的原因 | |
| B. | 亚里士多德认为力是维持物体运动的原因 | |
| C. | 笛卡尔通过扭秤实验第一个测出万有引力常量G的值 | |
| D. | 伽利略通过实验及合理外推,指出自由落体运动是一种匀变速直线运动 |
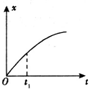
12.如图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其υ-t图象如图乙所示,同时人顶着杆沿水平地面运动的x-t图象如图丙所示.若以地面为参考系,下列说法正确的是( )
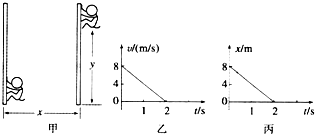

| A. | 猴子的运动轨迹为直线 | B. | 猴子在2s内做匀变速曲线运动 | ||
| C. | t=0时猴子的速度大小为8m/s | D. | 猴子在2s内的加速度大小为4m/s2 |
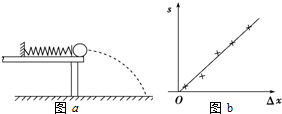 某同学利用图a装置探究轻质弹簧的弹性势能与弹簧形变量之间的关系.一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连:弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示.向左推小球,使弹簧压缩一段距离后由静止释放.小球离开桌面后落到水平地面上.通过测量和计算,可求得弹簧被压缩后的弹性势能.
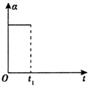
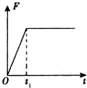
某同学利用图a装置探究轻质弹簧的弹性势能与弹簧形变量之间的关系.一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连:弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示.向左推小球,使弹簧压缩一段距离后由静止释放.小球离开桌面后落到水平地面上.通过测量和计算,可求得弹簧被压缩后的弹性势能.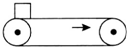 如图所示,一足够长的水平传送带以恒定的速度向右传动.将一物体轻轻放在皮带左端,以v、a、x、F表示物体速度大小、加速度大小、位移大小和所受摩擦力的大小.下列选项正确的是( )
如图所示,一足够长的水平传送带以恒定的速度向右传动.将一物体轻轻放在皮带左端,以v、a、x、F表示物体速度大小、加速度大小、位移大小和所受摩擦力的大小.下列选项正确的是( )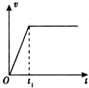

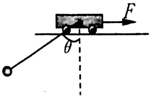 如图所示,天车质量为M=40kg,可沿着光滑的水平轨道运动.天车上拴着一根长为 L=40m的不可伸长的轻绳,轻绳另一端拴着一个质量为m=20kg的小球,现控制小球使轻绳偏离竖直方向60°角处于自然伸直状态,球与天车均静止.给天车施加一水平向右的恒力F的同时放开小球,运动中两者恰好能保持相对静止.当天车运动了d=5$\sqrt{3}$m时撤去F,同时锁定天车.不计空气阻力,取重力加速度g=10m/s2.请通过计算回答下列问题:
如图所示,天车质量为M=40kg,可沿着光滑的水平轨道运动.天车上拴着一根长为 L=40m的不可伸长的轻绳,轻绳另一端拴着一个质量为m=20kg的小球,现控制小球使轻绳偏离竖直方向60°角处于自然伸直状态,球与天车均静止.给天车施加一水平向右的恒力F的同时放开小球,运动中两者恰好能保持相对静止.当天车运动了d=5$\sqrt{3}$m时撤去F,同时锁定天车.不计空气阻力,取重力加速度g=10m/s2.请通过计算回答下列问题: