题目内容
(临界速度问题)在光滑的水平轨道上有两个半径都是r的小球A和B，质量分别为m和2 m，当两球心的距离大于l(l比2r大得多)时，两球之间无相互作用力．当两球心间的距离等于或小于l时，两球之间存在相互作用的恒定斥力F．设A球从远离B球处以速度v0沿两球心连线向原来静止的B球运动．如图所示．欲使两球不发生接触，v0必须满足什么条件？
答案：
解析：
解析：
解析：两球不相接触的条件是两球心间的距离d＞2r．
两球运动分析：当球心距离小于l后，A球受到斥力而做匀减速直线运动，B球受到斥力而做初速为零的匀加速运动，从而产生A追B的情形．开始阶段A球的速度大于B球速度，球间距离在减小．当B球速度大于A球速度时两球间的距离就会增大，所以两球的速度相等时两球间的距离达到最小．不相撞的条件是这个最小距离要大于2r．如图所示．
两球从相互作用开始，A的位移为xA，B的位移为xB，d＝xB＋l－xA＞2r．
解法Ⅰ：利用牛顿定律和运动学公式．
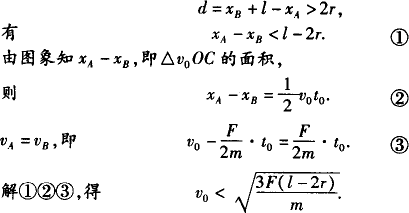
点评：解决此题的关键是对题目的物理过程进行分析，找出两球不相撞的条件．此题是动力学的综合题目，从不同的角度、不同的物理观点出发得到几种不同的解法，但各种解法中都应用了追击问题中当物体速度相等时，两物体间距最小这一临界条件．此题中l比2r大得多，但r不能忽略，即小球不能看成质点．本题考查应用牛顿运动定律与运动学公式进行分析和解决问题的能力，弄清物理过程，找出不接触的条件，v相同，l＋sB－sA＞2r是解题的关键．
练习册系列答案
步步高达标卷系列答案
相关题目
（2013?威海模拟）如图所示，两完全相同的小车A、B以大小相同的速度v0在光滑的水平面上相向运动，在A车上有一质量为m的小木块与A车保持相对静止，小车的质量为M，且M=2m．两小车发生碰撞后，A车立即停止，小木块滑上B车，在 B车碰墙之前与B车达到共同速度．小车B与右侧的墙壁发生完全弹性碰撞后很快与小木块一起向左运动．求它们一起向左运动的速度大小．