题目内容
3. 静止在地面上的物块在F=1.6N的水平恒力作用下启动,运动一段时间后撤去F.此时物块运动了S=2m,已知物块质量M=0.2kg,与地面间的动摩擦因数μ=0.4.(取g=10m/s2)求F作用时间;若物块运动到A点后,速度v=2.4m/s,右侧用平滑的圆弧连接一倾角为37°的斜面,若斜面与物体间动摩擦因数为0.5,物块经0.34s经过B点,AB间距离为多少?
静止在地面上的物块在F=1.6N的水平恒力作用下启动,运动一段时间后撤去F.此时物块运动了S=2m,已知物块质量M=0.2kg,与地面间的动摩擦因数μ=0.4.(取g=10m/s2)求F作用时间;若物块运动到A点后,速度v=2.4m/s,右侧用平滑的圆弧连接一倾角为37°的斜面,若斜面与物体间动摩擦因数为0.5,物块经0.34s经过B点,AB间距离为多少?
分析 (1)对物体进行受力分析,由动能定理即可求出物体的速度,然后又动量定理即可求出作用的时间;
(2)对斜面上的物体进行受力分析,由牛顿第二定律求出加速度,然后由位移公式即可求出.
解答 解:(1)水平面上的物体受到重力、支持力、摩擦力和拉力的作用,竖直方向支持力等于重力,水平方向:
由动量定理得:(F-μ1FN)•t1=mv1
代入数据得:t1=5s
(2)选取沿斜面向上的方向为正方向,则:
-mgsinθ-μ2mgcosθ=ma
代入数据,得:a=-10m/s2
物体向上运动的时间:${t}_{2}=\frac{△{v}_{1}}{a}=\frac{0-2.4}{-10}=0.24$s
所以物体到达最高点后,还要向下运动:t2=t0-t1=0.34-0.24=0.10s
物体向上运动的最大位移:${x}_{1}={v}_{0}{t}_{1}+\frac{1}{2}a{t}_{1}^{2}$=$2.4×0.24+\frac{1}{2}×(-10)×0.2{4}^{2}=0.288$m
物体向下运动的过程中:-mgsinθ+μ2mgcosθ=ma′
代入数据得:a′=-2m/s2
物体向下运动的位移:${x}_{2}=\frac{1}{2}a′{t}_{2}^{2}=\frac{1}{2}×(-2)×0.{1}^{2}=-0.01$m
所以物体向上运动的总位移:x=x1+x2=0.288+(-0.01)=0.287m
即AB间距离为0.287m
答:F作用的时间是5s;AB间距离为0.287m
点评 该题中的两问属于两个不同的情景,要结合题目中的情况,先对物体进行受力分析,然后结合题目的要求,再选择合适的公式即可正确解答.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.探究“合力做功的物体速度变化的关系”的实验中,小车会受到摩擦力的作用,可以使木板适当倾斜来平衡摩擦力,则下面操作正确的是( )
| A. | 放开小车,小车能够自由下滑即可 | |
| B. | 放开小车,小车能够匀速下滑即可 | |
| C. | 放开拖着纸带的小车,小车能够自由下滑即可 | |
| D. | 放开拖着纸带的小车,小车能够匀速下滑即可 |
11.下列关于地球同步卫星的说法正确的是( )
| A. | 它的周期和地球自转周期相同,但高度和速度可以选择,高度增大,速度减小 | |
| B. | 它的高度和速度是一定的,但周期可以是地球自转周期的整数倍 | |
| C. | 我国发射的同步卫星都定点在北京上空 | |
| D. | 我国发射的同步卫星都定点在赤道上空 |
15. 如图所示,平行且等间距的一组实线可能是电场线也可能是等势线,虚线是一电子在电场中以一定的初速度只在电场力的作用下由a点运动到b点的轨迹.则下列说法中正确的是( )
如图所示,平行且等间距的一组实线可能是电场线也可能是等势线,虚线是一电子在电场中以一定的初速度只在电场力的作用下由a点运动到b点的轨迹.则下列说法中正确的是( )
 如图所示,平行且等间距的一组实线可能是电场线也可能是等势线,虚线是一电子在电场中以一定的初速度只在电场力的作用下由a点运动到b点的轨迹.则下列说法中正确的是( )
如图所示,平行且等间距的一组实线可能是电场线也可能是等势线,虚线是一电子在电场中以一定的初速度只在电场力的作用下由a点运动到b点的轨迹.则下列说法中正确的是( )| A. | a点的电势比b点高 | |
| B. | 电子从a点到b点动能减小,电势能增加 | |
| C. | 电子从a点到b点做匀变速曲线运动 | |
| D. | 电子在a点的动能和电势能之和大于电子在b点动能和电势能之和 |

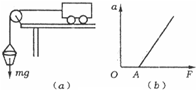 如图中(a)所示是“探究质量一定的物体加速度与作用力的关系”实验装置.研究对象是放在长木板上的小车,小车的质量为m,长木板水平放置,小车前端拴着细轻绳,跨过定滑轮,下面吊着砂桶,当砂和桶总质量远小于(填“等于”、“远大于”或“远小于”)小车质量时,可认为细绳对小车的作用力等于砂和桶的总重力mg,用改变砂子质量的办法,来改变对小车的作用力F,用打点计时器测出小车的加速度a,得出若干组F和a的数据,画出a-F图线(如图(b)所示).分析这一图线,直线明显没有通过原点,这不符合牛顿第二定律的a和F的正比关系,这是因为在实验中未平衡摩擦力或平衡不足.实验中平衡摩擦力时应稍微抬高木板无滑轮端使得不挂砂桶(选填“挂砂桶”或“不挂砂桶”)的小车在木板上匀速下行.
如图中(a)所示是“探究质量一定的物体加速度与作用力的关系”实验装置.研究对象是放在长木板上的小车,小车的质量为m,长木板水平放置,小车前端拴着细轻绳,跨过定滑轮,下面吊着砂桶,当砂和桶总质量远小于(填“等于”、“远大于”或“远小于”)小车质量时,可认为细绳对小车的作用力等于砂和桶的总重力mg,用改变砂子质量的办法,来改变对小车的作用力F,用打点计时器测出小车的加速度a,得出若干组F和a的数据,画出a-F图线(如图(b)所示).分析这一图线,直线明显没有通过原点,这不符合牛顿第二定律的a和F的正比关系,这是因为在实验中未平衡摩擦力或平衡不足.实验中平衡摩擦力时应稍微抬高木板无滑轮端使得不挂砂桶(选填“挂砂桶”或“不挂砂桶”)的小车在木板上匀速下行. 探究某种笔的弹跳问题时,把笔分为轻质弹簧、内芯和外壳三部分,其中内芯和外壳质量分别为m和4m.笔的弹跳过程分为三个阶段:①把笔竖直倒立于水平硬桌面,下压外壳使其下端接触桌面(见图a);②由静止释放,外壳竖直上升至下端距桌面高度为h1时,与静止的内芯碰撞(见图b);③碰后,内芯与外壳以共同的速度一起上升到外壳下端距桌面最大高度为h2处(见图c).设内芯与外壳的撞击力远大于笔所受重力、不计摩擦与空气阻力,重力加速度为g.求:外壳与碰撞后瞬间的共同速度大小.
探究某种笔的弹跳问题时,把笔分为轻质弹簧、内芯和外壳三部分,其中内芯和外壳质量分别为m和4m.笔的弹跳过程分为三个阶段:①把笔竖直倒立于水平硬桌面,下压外壳使其下端接触桌面(见图a);②由静止释放,外壳竖直上升至下端距桌面高度为h1时,与静止的内芯碰撞(见图b);③碰后,内芯与外壳以共同的速度一起上升到外壳下端距桌面最大高度为h2处(见图c).设内芯与外壳的撞击力远大于笔所受重力、不计摩擦与空气阻力,重力加速度为g.求:外壳与碰撞后瞬间的共同速度大小. 气缸长为L=1m(气缸厚度可忽略不计),固定在水平面上,气缸中有横街面积为S=100cm2的光滑活塞封闭了一定质量的理想气体.已知当温度t=27℃,大气压强p0=1×105Pa时,气柱长度l0=0.4m,现用水平拉力向右缓慢拉动活塞,求:
气缸长为L=1m(气缸厚度可忽略不计),固定在水平面上,气缸中有横街面积为S=100cm2的光滑活塞封闭了一定质量的理想气体.已知当温度t=27℃,大气压强p0=1×105Pa时,气柱长度l0=0.4m,现用水平拉力向右缓慢拉动活塞,求: 如图所示,在边长为L的正方形区域ABCD内,存在沿AD方向的匀强电场,质量均为m,带电量分别为+q和-q的两粒子,同时由A、C两点沿AB和CD方向以速率v0进入正方形区域,两粒子在区域的正中心相遇.若将区域中的电场换为垂直纸面向外的匀强磁场,两粒子同时由A、B两点沿平行于AB方向进入区域,速度大小仍为v0,两粒子也在区域的正中心相遇,不计粒子的重力和粒子间的相互作用力,求:
如图所示,在边长为L的正方形区域ABCD内,存在沿AD方向的匀强电场,质量均为m,带电量分别为+q和-q的两粒子,同时由A、C两点沿AB和CD方向以速率v0进入正方形区域,两粒子在区域的正中心相遇.若将区域中的电场换为垂直纸面向外的匀强磁场,两粒子同时由A、B两点沿平行于AB方向进入区域,速度大小仍为v0,两粒子也在区域的正中心相遇,不计粒子的重力和粒子间的相互作用力,求: