题目内容
3. 如图所示,物块a,b,c的质量关系ma:mb:mc=1;2:3,a和b、b和c之间用完全相同的轻弹簧S1和S2相连,通过系在a上的细线悬挂于固定点O.整个系统处于静止状态.现将细线剪断.将物块a的加速度的大小记为a1,S1和S2相对于原长的伸长分别记为△l1和△l2,重力加速度大小为g.在剪断的瞬间,( )
如图所示,物块a,b,c的质量关系ma:mb:mc=1;2:3,a和b、b和c之间用完全相同的轻弹簧S1和S2相连,通过系在a上的细线悬挂于固定点O.整个系统处于静止状态.现将细线剪断.将物块a的加速度的大小记为a1,S1和S2相对于原长的伸长分别记为△l1和△l2,重力加速度大小为g.在剪断的瞬间,( )| A. | a1=5g | B. | a1=6g | C. | 3△l1=2△l2 | D. | 3△l1=5△l2 |
分析 对细线剪短前后的a、b、c物体分别受力分析,然后根据牛顿第二定律求解加速度与弹簧的伸长量.
解答 解:AB、对a、b、c分别受力分析如图,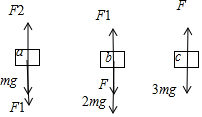
根据平衡条件,有:
对a:F2=F1+mg
对b:F1=F+2mg
对c:F=3mg
所以:F1=5mg
弹簧的弹力不能突变,因形变需要过程,绳的弹力可以突变,绳断拉力立即为零.
当绳断后,b与c受力不变,仍然平衡,故b的加速度a2=0;
对a,绳断后合力为F合=F1+mg=6mg=ma1,a1=6g方向竖直向下;故A错误,B正确.
CD、当绳断后,b与c受力不变,则F1=k△s1,△s1=$\frac{5mg}{k}$;同时:F=k△s2,所以:△s2=$\frac{3mg}{k}$.联立得3△l1=5△l2:故C错误,D正确.
故选:BD.
点评 本题考查了牛顿第二定律的瞬时性的应用,解题重点区分绳和弹簧弹力的特点,注意加速度与受力的瞬时对应关系.

练习册系列答案
相关题目
1. 一轿车和一货车在两条平行直道上同向行驶,开始时两车速度都为v0且轿车司机处于货车车尾并排位置,如图所示,为了超车,轿车司机开始控制轿车做匀加速运动,经过一段时间t,轿车司机到达货车车头并排位置,若货车车身长度为L,且货车保持匀速,则轿车加速过程的加速度大小为( )
一轿车和一货车在两条平行直道上同向行驶,开始时两车速度都为v0且轿车司机处于货车车尾并排位置,如图所示,为了超车,轿车司机开始控制轿车做匀加速运动,经过一段时间t,轿车司机到达货车车头并排位置,若货车车身长度为L,且货车保持匀速,则轿车加速过程的加速度大小为( )
 一轿车和一货车在两条平行直道上同向行驶,开始时两车速度都为v0且轿车司机处于货车车尾并排位置,如图所示,为了超车,轿车司机开始控制轿车做匀加速运动,经过一段时间t,轿车司机到达货车车头并排位置,若货车车身长度为L,且货车保持匀速,则轿车加速过程的加速度大小为( )
一轿车和一货车在两条平行直道上同向行驶,开始时两车速度都为v0且轿车司机处于货车车尾并排位置,如图所示,为了超车,轿车司机开始控制轿车做匀加速运动,经过一段时间t,轿车司机到达货车车头并排位置,若货车车身长度为L,且货车保持匀速,则轿车加速过程的加速度大小为( )| A. | $\frac{L}{{t}^{2}}$ | B. | $\frac{2L}{{t}^{2}}$ | C. | $\frac{{2(v}_{0}t+L)}{{t}^{2}}$ | D. | $\frac{{(v}_{0}t+L)}{{t}^{2}}$ |
2. 2016年12月23日日据《科技日报》今日报道,使用传统火箭的时候,从地球出发前往火星的单程“旅行”大约是6到7个月,相比传统引擎,如果电磁驱动引擎能够成功投入实际运动,人类可以在10个星期内抵达火星.中国已经开发了低轨道太空测试设备,目前安装在了天宫二号上进行测试,处于领先地位.若能将飞行器P送到火星附近使其绕火星做匀速圆周运动.如图所示,火星相对飞行器的张角为θ,火星半径为R,飞行器绕火星做匀速圆周运动的轨迹半径为r,若想求得火星的质量,下列条件满足的是( )
2016年12月23日日据《科技日报》今日报道,使用传统火箭的时候,从地球出发前往火星的单程“旅行”大约是6到7个月,相比传统引擎,如果电磁驱动引擎能够成功投入实际运动,人类可以在10个星期内抵达火星.中国已经开发了低轨道太空测试设备,目前安装在了天宫二号上进行测试,处于领先地位.若能将飞行器P送到火星附近使其绕火星做匀速圆周运动.如图所示,火星相对飞行器的张角为θ,火星半径为R,飞行器绕火星做匀速圆周运动的轨迹半径为r,若想求得火星的质量,下列条件满足的是( )
 2016年12月23日日据《科技日报》今日报道,使用传统火箭的时候,从地球出发前往火星的单程“旅行”大约是6到7个月,相比传统引擎,如果电磁驱动引擎能够成功投入实际运动,人类可以在10个星期内抵达火星.中国已经开发了低轨道太空测试设备,目前安装在了天宫二号上进行测试,处于领先地位.若能将飞行器P送到火星附近使其绕火星做匀速圆周运动.如图所示,火星相对飞行器的张角为θ,火星半径为R,飞行器绕火星做匀速圆周运动的轨迹半径为r,若想求得火星的质量,下列条件满足的是( )
2016年12月23日日据《科技日报》今日报道,使用传统火箭的时候,从地球出发前往火星的单程“旅行”大约是6到7个月,相比传统引擎,如果电磁驱动引擎能够成功投入实际运动,人类可以在10个星期内抵达火星.中国已经开发了低轨道太空测试设备,目前安装在了天宫二号上进行测试,处于领先地位.若能将飞行器P送到火星附近使其绕火星做匀速圆周运动.如图所示,火星相对飞行器的张角为θ,火星半径为R,飞行器绕火星做匀速圆周运动的轨迹半径为r,若想求得火星的质量,下列条件满足的是( )| A. | 若测得飞行器周期和火星半径R,可得到火星的质量 | |
| B. | 若测得飞行器周期和轨道半径r,可得到火星的质量 | |
| C. | 若测得飞行器周期和张角θ,可得到火星的质量 | |
| D. | 以上条件都不能单独得到火星的质量 |
19.用同种材料制成倾角为30°的斜面和长水平面,斜面长2.4m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0=2m/s时,经过0.8s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象,如图所示,则下列说法中正确的是(g=10m/s2)( )
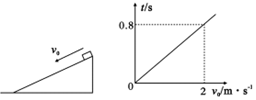

| A. | 小物块在斜面上运动时加速度大小为2.5m/s2 | |
| B. | 小物块在斜面上运动时加速度大小为0.4m/s2 | |
| C. | 小物块与该种材料间的动摩擦因数为0.5 | |
| D. | 由图可推断若小物块初速度继续增大,小物块的运动时间也随速度均匀增大 |
6. 将一轻质弹簧固定在竖直的墙壁上,如图所示,右端与一小球相连接,另用一质量不计且不可伸长的细绳与小球相连,另一端如图固定,当系统静止时水平面对小球的支持力为零,细绳与竖直方向的夹角θ=45°,小球与水平面间的摩擦不可忽略,且动摩擦因数μ=0.2,小球的质量为m=1kg,重力加速度取g=10m/s2,假设最大静摩擦力等于滑动摩擦力,则剪断细绳的瞬间,下列说法正确的是( )
将一轻质弹簧固定在竖直的墙壁上,如图所示,右端与一小球相连接,另用一质量不计且不可伸长的细绳与小球相连,另一端如图固定,当系统静止时水平面对小球的支持力为零,细绳与竖直方向的夹角θ=45°,小球与水平面间的摩擦不可忽略,且动摩擦因数μ=0.2,小球的质量为m=1kg,重力加速度取g=10m/s2,假设最大静摩擦力等于滑动摩擦力,则剪断细绳的瞬间,下列说法正确的是( )
 将一轻质弹簧固定在竖直的墙壁上,如图所示,右端与一小球相连接,另用一质量不计且不可伸长的细绳与小球相连,另一端如图固定,当系统静止时水平面对小球的支持力为零,细绳与竖直方向的夹角θ=45°,小球与水平面间的摩擦不可忽略,且动摩擦因数μ=0.2,小球的质量为m=1kg,重力加速度取g=10m/s2,假设最大静摩擦力等于滑动摩擦力,则剪断细绳的瞬间,下列说法正确的是( )
将一轻质弹簧固定在竖直的墙壁上,如图所示,右端与一小球相连接,另用一质量不计且不可伸长的细绳与小球相连,另一端如图固定,当系统静止时水平面对小球的支持力为零,细绳与竖直方向的夹角θ=45°,小球与水平面间的摩擦不可忽略,且动摩擦因数μ=0.2,小球的质量为m=1kg,重力加速度取g=10m/s2,假设最大静摩擦力等于滑动摩擦力,则剪断细绳的瞬间,下列说法正确的是( )| A. | 小球仍处于静止状态 | B. | 小球所受合力为10N | ||
| C. | 小球的加速度大小为8m/s2 | D. | 小球所受的摩擦力为零 |
8.根据如表提供的信息回答.(提示:表格中第3行“20”“30”表示速度,它们下面的数据表示制动距离)(结果保留一位小数)
(1)从表中查出质量为4.5t的汽车,以20km/h的速度空载行驶时的制动距离,求地面对汽车的阻力不得小于多少?
(2)从表中查出一辆总质量4.0t的轿车,以30km/h的速度满载行驶时的制动距离,若该轿车以60km/h速度行驶,求其满载时制动距离允许最大值是多大?
| 机动车的类型 | 各检验项目和速度限值v/(km•h-1) | |||
| 空载检验的制动距离x/m | 满载检验的制动距离x/m | |||
| 20km•h-1 | 30km•h-1 | 20km•h-1 | 30km•h-1 | |
| 总质量<4.5t | ≤6.5 | ≤7.0 | ||
| 4.5t≤总质量≤12t的汽车和无轨电车 | ≤3.8 | ≤8.0 | ||
| 总质量>12t的汽车和无轨电车 | ≤4.4 | ≤9.5 | ||
(2)从表中查出一辆总质量4.0t的轿车,以30km/h的速度满载行驶时的制动距离,若该轿车以60km/h速度行驶,求其满载时制动距离允许最大值是多大?
15.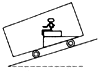 为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )
为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )
 为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )
为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )| A. | 乘客所受合外力可能竖直向下 | B. | 支持力可能大于重力 | ||
| C. | 受到向前(水平向左)的摩擦力作用 | D. | 可能处于超重状态 |
12.有两个惯性参考系1和2,彼此相对做匀速直线运动,下列叙述正确的是( )
| A. | 在参考系1看来,2中的所有物理过程都变快了;在参考系2看来,1中的所有物理过程都变慢了 | |
| B. | 在参考系1看来,2中的所有物理过程都变快了;在参考系2看来,1中的所有物理过程也变快了 | |
| C. | 在参考系1看来,2中的所有物理过程都变慢了;在参考系2看来,1中的所有物理过程都变快了 | |
| D. | 在参考系1看来,2中的所有物理过程都变慢了;在参考系2看来,1中的所有物理过程也变慢了 |
13.G20峰会于2016年9月初在杭州奥体博览城召开,某记者从萧山国际机场到博览城打车约23.5km,峰会期间的文艺演出于北京时间9月4日21:15正式上演.则下列说法正确的是( )
| A. | 9 月 4 日 21:15 指时间间隔,23.5km 指路程 | |
| B. | 9 月 4 日 21:15 指时刻,23.5km 指路程 | |
| C. | 9 月 4 日 21:15 指时间间隔,23.5km 指位移大小 | |
| D. | 9 月 4 日 21:15 指时刻,23.5km 指位移大小 |