题目内容
1. 如图所示,A、B、C、D、E、F为匀强电场中一个边长为10cm的正六边形的六个顶点,A、B、C三点电势分别为1.0V、2.0V、3.0V,则下列说法正确的是( )
如图所示,A、B、C、D、E、F为匀强电场中一个边长为10cm的正六边形的六个顶点,A、B、C三点电势分别为1.0V、2.0V、3.0V,则下列说法正确的是( )| A. | 匀强电场的电场强度大小为10 V/m | |
| B. | 匀强电场的电场强度大小为$\frac{20\sqrt{3}}{3}$ V/m | |
| C. | 电荷量为1.6×10-19 C的正点电荷从E点移到F点,电荷克服电场力做功为1.6×10-19 J | |
| D. | 电荷量为1.6×10-19 C的负点电荷从F点移到D点,电荷的电势能减少4.8×10-19 J |
分析 连接AC,根据匀强电场电势随距离均匀变化(除等势面)的特点,AC中点的电势为2V,则EB为一条等势线,CA连线即为一条电场线,由BA间的电势差,由公式U=Ed求出场强大小.AF∥EB,则知AF也为一条等势线,可求出UEF,电场力做功就可以求解.
解答 解:AB、连接AC,AC中点电势为2V,与B电势相等,则EB连线必为一条等势线,BA间的电势差为UBA=1V,又UBA=EdABcos30°,得场强为:
E=$\frac{{U}_{AB}}{{d}_{AB}cos30°}$=$\frac{1}{0.1×\frac{\sqrt{3}}{2}}$=$\frac{20\sqrt{3}}{3}$ V/m.故A错误,B正确.
C、由正六边形对称性,EB∥AF,则AF也为电场中的一条等势线,φF=φA=1V,由上可知,E的电势为φE=φB=2V>φF,则电荷量为1.6×10-19C的正点电荷从E点移到F点,电场力做正功,而且为WEF=qUEF=q(φE-φF)=1.6×10-19×(2-1)J=1.6×10-19J,故C错误.
D、D点的电势等于C点的电势,φD=3V,电荷量为1.6×10-19C的负点电荷从F点移到D点,电场力做功为WFD=qUFD=q(φF-φD)=-1.6×10-19×(1-3)J=3.2×10-19J,电势能减小3.2×10-19J.故D错误.
故选:B
点评 找等势点,作出电场线,是解决这类问题常用方法.本题还要充分利用正六边形的对称性分析匀强电场中各点电势的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.关于温度的下列说法,正确的是( )
| A. | 温度是物体的冷热程度的标志 | |
| B. | 温度是物体内能的标志 | |
| C. | 温度是物体分子势能的标志 | |
| D. | 气体的温度是气体分子平均动能的标志 |
12.两个电源的伏安特征图线如图所示,由图可知( )


| A. | 电源a的电动势较大 | B. | 电源b的电动势较大 | ||
| C. | 电源a的内电阻较小 | D. | 电源b的内电阻较小 |
9.将两个半径极小的带电小球(可视为点电荷)置于一个绝缘的光滑水平面上,从静止开始释放,那么下列叙述中正确的是(忽略万有引力)( )
| A. | 它们的加速度一定在同一直线上,而且方向可能相同 | |
| B. | 它们的加速度可能为零 | |
| C. | 它们的加速度方向一定相反 | |
| D. | 它们的加速度大小一定越来越小 |
16.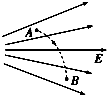 一带电粒子从电场中的A点运动到B点,径迹如图中虚线所示,不计粒子所受重力,下列说法不正确的是( )
一带电粒子从电场中的A点运动到B点,径迹如图中虚线所示,不计粒子所受重力,下列说法不正确的是( )
 一带电粒子从电场中的A点运动到B点,径迹如图中虚线所示,不计粒子所受重力,下列说法不正确的是( )
一带电粒子从电场中的A点运动到B点,径迹如图中虚线所示,不计粒子所受重力,下列说法不正确的是( )| A. | 粒子带负电 | B. | 粒子加速度逐渐减小 | ||
| C. | A点的场强大于B点场强 | D. | 粒子的速度不断增大 |
6.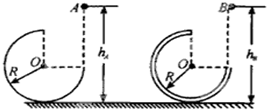 如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )
如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )
 如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )
如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )| A. | 适当调整hA和hB,均可使两小球从轨道最高点飞出后,恰好落在轨道右端口处 | |
| B. | 若hA=hB=2R,则两小球在轨道最低点对轨道的压力为4mg | |
| C. | 若hA=hB=R,则两小球都能上升到离地高度为R的位置 | |
| D. | 若使小球沿轨道运动并且能从最高点飞出,A小球的最小高度为$\frac{5B}{2}$,B小球在hB>2R的任何高度均可 |
13.在单杠上做引体向上时,甲同学两手距离与肩同宽,乙同学两手距离大于肩宽,设甲、乙两人的质量相同,则以下说法正确的是( )
| A. | 甲同学更省力 | B. | 乙同学更省力 | C. | 两同学一样省力 | D. | 无法比较 |
10.有两个跨度较大的山头,将照明线路的导线经过这两个山头架设,为使导线不被拉断,则下列说法正确的是( )
| A. | 导线是否被拉断,只与山头间的距离有关,与导线的松紧无关 | |
| B. | 尽可能拉紧导线,以使减小导线的长度,从而减小导线的自身的重量 | |
| C. | 尽可能的松一些,导线弯曲程度越大,两端拉力的角度就越小,需要的力也就越小 | |
| D. | 适量的松一些 |
11. 电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:
电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:
电流表A:量程0〜600mA,内阻约2Ω
电流表G:量程0〜500 ?A,内阻Rg=200Ω
电压表V:量程0〜3V,内阻约5kΩ
定值电阻R1=19800Ω
定值电阻R2=9800Ω
滑动变阻器R3:0〜100Ω,1A
滑动变阻器R4:0〜1000Ω,1A
电键一只,导线若干
待测电瓶E
(1)请选择合适的器材在下边虚线框中画出实验电路图(器材必须标明符号).
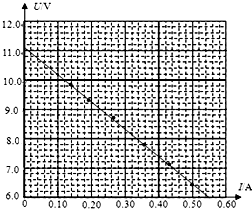
(2)兴趣小组记录了实验数据,并通过计算得到了6组电压U和对应电流I的值,作出了U-I图象.由图象可得这块旧电瓶的电动势为11.1V,内阻为9.5Ω
 电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:
电动自行车的一块电瓶标称电动势为12V,但用久以后性能会下降.表现之一为电瓶的电动势变小,内阻变大.某兴趣小组将某电动自行车的一块旧电瓶充满电后测量它的电动势和内阻.现有下列器材可用:电流表A:量程0〜600mA,内阻约2Ω
电流表G:量程0〜500 ?A,内阻Rg=200Ω
电压表V:量程0〜3V,内阻约5kΩ
定值电阻R1=19800Ω
定值电阻R2=9800Ω
滑动变阻器R3:0〜100Ω,1A
滑动变阻器R4:0〜1000Ω,1A
电键一只,导线若干
待测电瓶E
(1)请选择合适的器材在下边虚线框中画出实验电路图(器材必须标明符号).
(2)兴趣小组记录了实验数据,并通过计算得到了6组电压U和对应电流I的值,作出了U-I图象.由图象可得这块旧电瓶的电动势为11.1V,内阻为9.5Ω
| 电压U/V | 9.80 | 9.30 | 8.70 | 7.80 | 7.13 | 6.42 |
| 电流I/A | 0.14 | 0.19 | 0.26 | 0.35 | 0.43 | 0.50 |