题目内容
17.某实验小组欲以如图1所示实验装置“探究加速度与物体受力和质量的关系”.图中A为小车,B为装有砝码的小盘,C为一端带有定滑轮的长木板,小车通过纸带与电磁打点计时器相连,小车的质量为m1,小盘(及砝码)的质量为m2.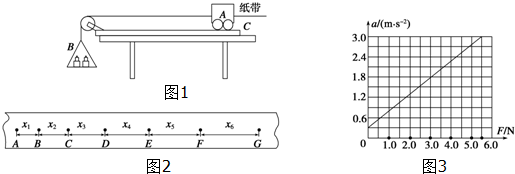
(1)下列说法正确的是C
A.实验时先放开小车,再接通打点计时器的电源
B.每次改变小车质量时,应重新平衡摩擦力
C.本实验中应满足m2远小于m1的条件
D.在用图象探究小车加速度与受力的关系时,应作a-m1图象
(2)实验中,得到一条打点的纸带,如图2所示,已知相邻计数点间的时间间隔为T,且间距x1、x2、x3、x4、x5、x6已量出,则打点计时器打下F点时小车的瞬时速度的计算式为vF=$\frac{{x}_{5}+{x}_{6}}{2T}$,小车加速度的计算式a=$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$.
(3)某同学平衡好摩擦阻力后,在保持小车质量不变的情况下,通过多次改变砝码重力,作出小车加速度a与砝码重力F的图象如图3所示.若牛顿第二定律成立,重力加速度g=10m/s2,则小车的质量为2.0kg,小盘的质量为0.06kg.
(4)实际上,在砝码的重力越来越大时,小车的加速度不能无限制地增大,将趋近于某一极限值,此极限值为10m/s2.
分析 (1)实验时需要提前做的工作有两个:①平衡摩擦力,且每次改变小车质量时,不用重新平衡摩擦力,因为f=mgsinθ=μmgcosθ,m约掉了.②让小车的质量M远远大于小盘和重物的质量m;
(2)根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上F点时小车的瞬时速度大小;
(3)由F-a图的斜率等于小车质量,可得到小车质量,F=0时,产生的加速度是由于托盘作用产生的,可得托盘质量;
(4)车在托盘和砝码带动下最大的加速度不会超过托盘和砝码下落的加速度,而此下落加速度的极值就是重力加速度.
解答 解:(1)A、实验时应先接通电源后释放小车,故A错误.
B、平衡摩擦力,假设木板倾角为θ,则有:f=mgsinθ=μmgcosθ,m约掉了,故不需要重新平衡摩擦力.故B错误.
C、让小车的质量m1远远大于小盘和重物的质量m2,因为:际上绳子的拉力F=Ma=$\frac{{m}_{2}g}{1+\frac{{m}_{2}}{{m}_{1}}}$,故应该是m2<<m1,即实验中应满足小盘和重物的质量远小于小车的质量,故C正确;
D、F=m1a,所以:a=$\frac{F}{{m}_{1}}$,所以在用图象探究小车的加速度与质量的关系时,通常作a-$\frac{1}{{m}_{1}}$图象,故D错误;
故选:C.
(2)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上F点时小车的瞬时速度大小.
vF=$\frac{{x}_{5}+{x}_{6}}{2T}$
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值得:
a=$\frac{1}{2}$(a1+a2+a3)=$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$
(3)对a-F图来说,图象的斜率表示小车质量的倒数,故小车质量为:m1=$\frac{5.5-0}{3-0.3}$=2.0kg,
F=0时,产生的加速度是由于托盘作用产生的,故有:mg=m1a0,
解得:m=$\frac{2×0.3}{10}$=0.06kg
(4)小车的加速度最大等于自由落体的加速度,故极限值为10m/s2.
故答案为:(1)C;(2)$\frac{{x}_{5}+{x}_{6}}{2T}$;$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$;(3)2.0;0.06;(4)10
点评 本题考察的比较综合,需要学生对这一实验掌握的非常熟,理解的比较深刻才不会出错,知道a-F图的斜率等于小车质量的倒数,难度适中.要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度V匀速向右运动时,物体A的速度情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度V匀速向右运动时,物体A的速度情况是( )| A. | 物体的速度始终大于V | B. | 物体的速度始终等于V | ||
| C. | 物体的速度始终小于V | D. | 物体的速度先大于V后变小于V |
| A. | 奥斯特实验--电磁铁 | |
| B. | 电磁感应--电动机 | |
| C. | 磁场对电流的作用--发电机 | |
| D. | 麦克斯韦的电磁场理论--无线电通讯 |
 如图所示,B、C、D三点都在以点电荷十Q为圆心的某同心圆弧上,将一试探电荷从A点分别移到B、C、D各点时,电场力做功大小比较( )
如图所示,B、C、D三点都在以点电荷十Q为圆心的某同心圆弧上,将一试探电荷从A点分别移到B、C、D各点时,电场力做功大小比较( )| A. | WAB>WAC | B. | WAB=WAC | C. | WAC=WAD | D. | WAD>WAB |

| A. | 该物体受到的合力为0 | |
| B. | 该物体受到的合力为F | |
| C. | 该物体受到的摩擦力比F大 | |
| D. | 该物体受到的摩擦力与物体重力成正比 |
| A. | 位移、时间、平均速度 | B. | 速度、路程、平均速度 | ||
| C. | 速率、加速度、路程 | D. | 位移、速度、加速度 |
