题目内容
9.某实验探究小组按照“探究加速度与物体质量、物体受力的关系”的实验要求按图a安装好实验装置,并且特别注意到在挂上钩码之前把木板的右端(打点计时器所在的端)适当垫高,让推动后的小车能带着纸带做匀速运动.此后挂上合适的钩码.并在小车上加上适量的法码.打开电源,让小车从静止开始运动.实验中,小车碰到左端的制动装置时,钩码尚未到达地面,断开电源取下纸带.改变钩码的质量重复以上测量过程.打点计时器工作频率为f=50Hz.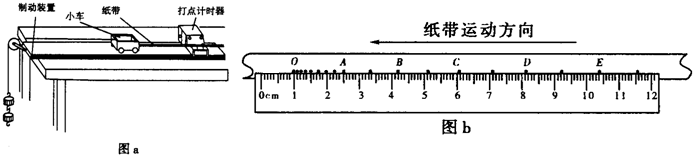
(1)设图b是钩码质量为m,小车与砝码的总质量为M时得到的一条纸带,在纸带上选择小车开始运动的起始点为O在此后打点比较清晰处再取A、B、C、D和E五个计数点,则C点位置在刻度尺上的读数为6.05cm.如果A、B、C、D、E各计数点到O点的距离分别记为d1、d2、d3、d4、d5、请利用这五个物理量和打点计时器的工作频率f
①写出一个能计算小车加速度表达式a=$\frac{{(d}_{4}+{d}_{2}-2{d}_{3}){f}^{2}}{4}$
②写出一个能计算小车过C点时的速度表达式Vc=$\frac{{(d}_{4}-{d}_{2})f}{4}$
(2)如果可以认为小车受到钩码的拉力F可以近似地等于钩码的重量mg,这个小组在做完验证牛顿运动定律实验之后认为还可以小车为研究对象利用上述数据来验证动能定理.你认为行吗?答行
①如果行请利用上述已有的物理量列出一个要验证的方程式$mg{d}_{3}=\frac{1}{2}M{[\frac{{(d}_{4}-{d}_{2})f}{4}]}^{2}$
②如果不行请简述理由
(3)指出认为小车受到钩码的拉力F可以近似地等于钩码的重量mg一个条件:M》m.
分析 (1)注意读数时要进行估读,由于小车做匀变速直线运动,根据时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出C点速度大小,利用逐差法△x=aT2求解加速度;
(2)可以验证动能定理,选择从O到C的过程中,求出合力做的功和动能的变化量,从而求出需要证明的表达式;
(3)当钩码质量m与小车质量M满足的条件是M>>m时可以认为小车受到钩码的拉力F可以近似地等于钩码的重量.
解答 解:根据刻度尺的读数可知,C点位置在刻度尺上的读数为6.05cm;
图中两个计数点之间的时间间隔T=$\frac{2}{f}$,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度a=$\frac{{d}_{4}+{d}_{2}-2{d}_{3}}{{T}^{2}}$=$\frac{{(d}_{4}+{d}_{2}-2{d}_{3}){f}^{2}}{4}$
根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出C点是速度为:
vC=$\frac{{x}_{BD}}{2T}=\frac{{(d}_{4}-{d}_{2})f}{4}$
(2)可以用上述数据来验证动能定理,
选择从O到C的过程中,合力做功W=mgd3,动能的变化量$△{E}_{K}=\frac{1}{2}M{{v}_{C}}^{2}-0=\frac{1}{2}M[\frac{{(d}_{4}-{d}_{2})f}{4}]^{2}$,
则要验证$mg{d}_{3}=\frac{1}{2}M{[\frac{{(d}_{4}-{d}_{2})f}{4}]}^{2}$即可;
(3)为了使轻绳的拉力可以近似认为等于钩码的重力,钩码质量m与小车质量M必须满足的条件是M>>m;
故答案为:(1)6.05;①$\frac{{(d}_{4}+{d}_{2}-2{d}_{3}){f}^{2}}{4}$; ②$\frac{{(d}_{4}-{d}_{2})f}{4}$;
(2)行;①$mg{d}_{3}=\frac{1}{2}M{[\frac{{(d}_{4}-{d}_{2})f}{4}]}^{2}$
(3)M》m.
点评 本题利用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,提高解决问题能力.

 如图所示,当左边线框通以逆时针方向的电流I时,天平恰好平衡.如改用等大顺时针方向的电流,则要在右边加挂质量△m的钩码,设匀强磁场磁感应强度为B,则线框的边长L=$\frac{2△mg}{BI}$.
如图所示,当左边线框通以逆时针方向的电流I时,天平恰好平衡.如改用等大顺时针方向的电流,则要在右边加挂质量△m的钩码,设匀强磁场磁感应强度为B,则线框的边长L=$\frac{2△mg}{BI}$.  如图所示为二种不同颜色的单色可见光a、b都垂直与相同棱镜的一个边入射入棱镜之后所做出的正确光路图(b光在底边发生全反射),则( )
如图所示为二种不同颜色的单色可见光a、b都垂直与相同棱镜的一个边入射入棱镜之后所做出的正确光路图(b光在底边发生全反射),则( )| A. | b光可能是红光 | |
| B. | 让这二种色光通过同一双缝干涉仪所产生的干涉条纹b光更宽 | |
| C. | 让这二种色光通过同一单缝,所产生的衍射现象a光更明显 | |
| D. | a光在棱镜中传播的速度小于b在棱镜中传播的速度 |
| A. | 温度不变,压强增加,放出热量 | B. | 温度增加,体积减小,吸收热量 | ||
| C. | 体积增加,压强减小,吸收热量 | D. | 温度不变,对外做功,放出热量 |
 如图所示,质量为m,带电量+q的小球置于半径为R的半圆形光滑轨道内,整个装置处于场强为E的竖直向下匀强电场中,小球从水平直径位置上的a点由静止释放,求小球经过最低点b时轨道对小球支持力的大小.(重力加速度为g)
如图所示,质量为m,带电量+q的小球置于半径为R的半圆形光滑轨道内,整个装置处于场强为E的竖直向下匀强电场中,小球从水平直径位置上的a点由静止释放,求小球经过最低点b时轨道对小球支持力的大小.(重力加速度为g)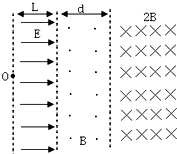 如图所示,某一空间分布着有理想边界的匀强电场和匀强磁场.左侧区域匀强电场的场强大小为E,方向水平向右,电场宽度为L;中间区域匀强磁场磁感应强度大小为B,方向垂直于纸面向外.右侧区域匀强磁场的磁感应强度大小为2B,方向垂直纸面向里,其右边界可向右边无限延伸.一个质量为m、带电量为+q的粒子(重力不计)从电场左边界上的O点由静止开始运动,穿过中间的磁场区域后进入右侧磁场区域,又回到O点,然后重复上述过程.求:
如图所示,某一空间分布着有理想边界的匀强电场和匀强磁场.左侧区域匀强电场的场强大小为E,方向水平向右,电场宽度为L;中间区域匀强磁场磁感应强度大小为B,方向垂直于纸面向外.右侧区域匀强磁场的磁感应强度大小为2B,方向垂直纸面向里,其右边界可向右边无限延伸.一个质量为m、带电量为+q的粒子(重力不计)从电场左边界上的O点由静止开始运动,穿过中间的磁场区域后进入右侧磁场区域,又回到O点,然后重复上述过程.求: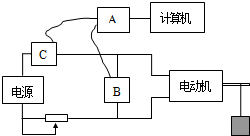 如图所示是利用DIS测定电动机效率的电路,试完成下列问题:
如图所示是利用DIS测定电动机效率的电路,试完成下列问题: