Question

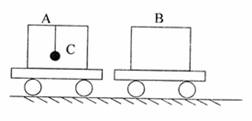
质量均为m，完全相同的两辆实验小车A和B停放在光滑水面上，A车上另悬挂有一质量为2m的小球C。开始B静止，A、C以速度v₀向右运动，两车发生完全非弹性碰撞但不粘连，碰撞时间极短，碰后小球C先向右摆起，再向左摆起每次均未达到水平，求：     

   （1）小球第一次向右摆起至最大高度h₁时小车A的速度大小v。

   （2）小球第一次向右摆起的最大高度h₁和第一次向左摆起的最大高度h₂之比。

Answer 1

解：

   （1）研究A、B、C整体，从最开始到小球第一次向右摆起至最大高度过程中，根据水平方向动量守恒

3mv₀ = 4m v

解得

   （2）研究A、B整体，两车碰撞过程中，设碰后瞬间A、B共同速度为v₁，根据动量守恒     mv₀ = (2m)v₁

解得   

从碰拉结束到小球第一次向右摆起至最大高度过程中，根据机械能守定律

      

解得

 由受力分析可知，小球下摆回最低点，B、C开始分离

 设此时小球速度为v₃，小车速度为v₄，以向右为正方向，从碰撞结束到小球摆回最低点过程中根据水平方向动量守恒 （2m）v₀ +(2m)v₁ = (2m)v₃ +(2m)v₄

 根据机械能守恒定律

 解得小球速度v₃ = v₁ =，方向向右，小车速度v₄ = v₀，方向向右

 另一根不合题意舍去。（用其它方法得出此结果同样得分）

 研究A、C整体，从返回最低点到摆到左侧最高点过程

 根据水平方向向量守恒  (2m) v₃ +mv₄ = (3m)v₅

 根据机械能守恒定律  

 解得，所以h₁：h₂ =3：2