题目内容
 如图所示,电荷量为e,质量为m的电子从A点沿与电场垂直的方向进入匀强电场,初速度为v0,当它通过电场中B点时,速度与场强方向成150°角,不计电子的重力,求:
如图所示,电荷量为e,质量为m的电子从A点沿与电场垂直的方向进入匀强电场,初速度为v0,当它通过电场中B点时,速度与场强方向成150°角,不计电子的重力,求:(1)B点的速度.
(2)A、B两点间的电势差.
分析:电子垂直进入匀强电场中,做类平抛运动,作出电子经过B点时速度的分解图,求出经过B点时的速度,根据动能定理求解A、B两点间的电势差
解答:解:(1)如图对末速度进行分解:cos60°=
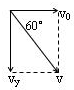
所以:v=
=2v0
(2)从A到B过程,由动能定理得:-eU=
mv2-
m
所以:U=-
答:B点的速度是2v0;A、B两点间的电势差为-
.
| v0 |
| v |

所以:v=
| v0 |
| cos60° |
(2)从A到B过程,由动能定理得:-eU=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
所以:U=-
3m
| ||
| 2e |
答:B点的速度是2v0;A、B两点间的电势差为-
3m
| ||
| 2e |
点评:本题运用动能定理求电势差,也可以根据类平抛运动的特点,牛顿第二定律和运动学结合求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
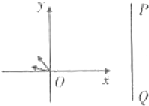 如图所示,电荷量为e、质量为m的质子从坐标原点O处沿xOy平面射入第二象限内的各个不同方向,射入时的速度大小均为v0.现在某一区域内加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度大小为B,若这些质子穿过磁场后都能垂直地射到与y轴平行的荧光屏PQ上,不计质子重力.求:
如图所示,电荷量为e、质量为m的质子从坐标原点O处沿xOy平面射入第二象限内的各个不同方向,射入时的速度大小均为v0.现在某一区域内加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度大小为B,若这些质子穿过磁场后都能垂直地射到与y轴平行的荧光屏PQ上,不计质子重力.求:
 如图所示,电荷量为-e、质量为m的电子从A点沿与电场垂直的方向进入匀强电场,初速度为v,当它通过电场B点时,速度与场强方向成150°角,不计电子的重力,求A、B两点间的电势差.
如图所示,电荷量为-e、质量为m的电子从A点沿与电场垂直的方向进入匀强电场,初速度为v,当它通过电场B点时,速度与场强方向成150°角,不计电子的重力,求A、B两点间的电势差.