题目内容
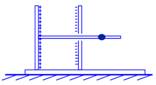
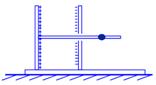
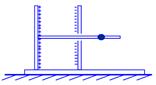
（本题12分） 固定有竖直电容器极板的绝缘底座放置在光滑的水平面上，板间距为d，一根光滑的绝缘杆穿过右极板的小孔水平固定在左极板上整体质量为M，电容器充电后，一质量为m的带正电小球套在杆上以一初速度v0，向左运动，已知运动中球与左端极板的最小距离为d/2，求距离最小时球的速度及该过程中电容器移动的距离。
距离最小时球的速度为v =
；电容器的位移大小为
解析:
由动量守恒可得 mv0＝（M+m）v 得距离最小时球的速度为v =
设者之间的相互作用力大小为F，对这一过程，由动能定理可得，
对M有 FSM＝
Mv2
对m有 －FSM＝mv2－mv02
又Sm－SM＝d/2 以上各式联立可得 电容器的位移大小为
练习册系列答案
相关题目
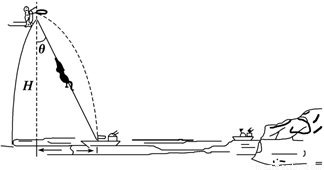
m/s平抛救生圈，第一个刚落到快艇，接着抛第二个，结果第二个救生圈刚好与甲队员同时抵达快艇，若人的质量为m，重力加速度g＝10 m/s2，问：
