题目内容
15.水利发电是利用水流的机械能发电,一小型发电机引水管截面积0.5m2,利用20m高处,流速2.2m/s的水流发电,出水口与入水口水流速相等,已知水的密度为1×103kg/m3发电机将机械能转化为电能的效率20%;发电机内阻不计,输出电压为220V,输电导线的电阻为0.2Ω,如果用原、副线圈匝数之比为1:10的升压变压器升压,经输电线路后,再用原、副线圈匝数比为10:1的降压变压器降压供给用户.(1)求发电机的输出功率;
(2)求用户得到的电压.
分析 (1)水的重力势能转化为电能,根据能量守恒求发电机的输出功率;
(2)画出全过程输电线路的电路图,整个电路由升压变压器与降压变压器,构成两个回路.由变压器的电压与匝数成正比,依据功率表达式P=UI,即可求解用户得到的电压.
解答 解:(1)发电机的输出功率为 P=ηρvSgh=20%×1×103×2.2×0.5×10×20W=4.4××104W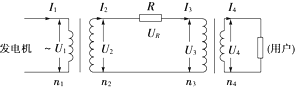
(2)画出全过程输电线路的电路图如图,R表示输电导线的等效电阻.
在升压变压器处,有$\frac{{U}_{1}}{{U}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$,得 U2=$\frac{{n}_{2}}{{n}_{1}}{U}_{1}$=10U1=2200V
输电线上电流 I2=$\frac{P}{{U}_{2}}$=$\frac{4.4×1{0}^{4}}{2200}$=20A
线路损失电压△U=I2R=20×0.2=4V
降压变压器处 U3=U2-△U=2200V-4=2196V;
由$\frac{{U}_{3}}{{U}_{4}}=\frac{{n}_{3}}{{n}_{4}}$得:U4=$\frac{{n}_{4}}{{n}_{3}}{U}_{3}$=$\frac{2196}{10}$V=219.6V
答:
(1)发电机的输出功率是4.4××104W;
(2)用户得到的电压是219.6V.
点评 本题的关键:1、正确分析能量是如何转化的.2、原副线圈的电压比、电流比与匝数比的关系;3、输送功率和输送电压、电流的关系.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
5.关于抛体运动,下列说法正确的是( )
| A. | 匀变速运动 | B. | 变加速运动 | ||
| C. | 物体一定做曲线运动 | D. | 物体可能做直线运动 |
10. 某电场的分布如图所示,带箭头的实线为电场线,虚线为等势面.A、B、C三点的电场强度分别为EA、EB、EC,电势分别为φA、φB、φC,关于这三点的电场强度和电势的关系,以下判断正确的是( )
某电场的分布如图所示,带箭头的实线为电场线,虚线为等势面.A、B、C三点的电场强度分别为EA、EB、EC,电势分别为φA、φB、φC,关于这三点的电场强度和电势的关系,以下判断正确的是( )
 某电场的分布如图所示,带箭头的实线为电场线,虚线为等势面.A、B、C三点的电场强度分别为EA、EB、EC,电势分别为φA、φB、φC,关于这三点的电场强度和电势的关系,以下判断正确的是( )
某电场的分布如图所示,带箭头的实线为电场线,虚线为等势面.A、B、C三点的电场强度分别为EA、EB、EC,电势分别为φA、φB、φC,关于这三点的电场强度和电势的关系,以下判断正确的是( )| A. | EA<EB,φB=φC | B. | EA>EB,φA<φB | C. | EA>EB,φA>φB | D. | EA=EC,φB=φC |
3. 如图所示,图甲中MN为足够大的不带电薄金属板,在金属板的右侧,距离为d的位置上放入一个电荷量为+q的点电荷O,由于静电感应产生了如图甲所示的电场分布.P是金属板上的一点,P点与点电荷O之间的距离为r,几位同学想求出P点的电场强度大小,但发现问题很难.几位同学经过仔细研究,从图乙所示的电场得到了一些启示,经过查阅资料他们知道:图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的.图乙中两异号点电荷电荷量的大小均为q,它们之间的距离为2d,虚线是两点电荷连线的中垂线.由此他们分别对P点的电场强度方向和大小做出以下判断,其中正确的是( )
如图所示,图甲中MN为足够大的不带电薄金属板,在金属板的右侧,距离为d的位置上放入一个电荷量为+q的点电荷O,由于静电感应产生了如图甲所示的电场分布.P是金属板上的一点,P点与点电荷O之间的距离为r,几位同学想求出P点的电场强度大小,但发现问题很难.几位同学经过仔细研究,从图乙所示的电场得到了一些启示,经过查阅资料他们知道:图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的.图乙中两异号点电荷电荷量的大小均为q,它们之间的距离为2d,虚线是两点电荷连线的中垂线.由此他们分别对P点的电场强度方向和大小做出以下判断,其中正确的是( )
 如图所示,图甲中MN为足够大的不带电薄金属板,在金属板的右侧,距离为d的位置上放入一个电荷量为+q的点电荷O,由于静电感应产生了如图甲所示的电场分布.P是金属板上的一点,P点与点电荷O之间的距离为r,几位同学想求出P点的电场强度大小,但发现问题很难.几位同学经过仔细研究,从图乙所示的电场得到了一些启示,经过查阅资料他们知道:图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的.图乙中两异号点电荷电荷量的大小均为q,它们之间的距离为2d,虚线是两点电荷连线的中垂线.由此他们分别对P点的电场强度方向和大小做出以下判断,其中正确的是( )
如图所示,图甲中MN为足够大的不带电薄金属板,在金属板的右侧,距离为d的位置上放入一个电荷量为+q的点电荷O,由于静电感应产生了如图甲所示的电场分布.P是金属板上的一点,P点与点电荷O之间的距离为r,几位同学想求出P点的电场强度大小,但发现问题很难.几位同学经过仔细研究,从图乙所示的电场得到了一些启示,经过查阅资料他们知道:图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的.图乙中两异号点电荷电荷量的大小均为q,它们之间的距离为2d,虚线是两点电荷连线的中垂线.由此他们分别对P点的电场强度方向和大小做出以下判断,其中正确的是( )| A. | 方向沿P点和点电荷的连线向左,大小为$\frac{2kqd}{{r}^{3}}$ | |
| B. | 方向沿P点和点电荷的连线向左,大小为$\frac{2kq\sqrt{{r}^{2}-{d}^{2}}}{{r}^{3}}$ | |
| C. | 方向垂直于金属板向左,大小为 $\frac{2kqd}{{r}^{3}}$ | |
| D. | 方向垂直于金属板向左,大小为 $\frac{2kq\sqrt{{r}^{2}-{d}^{2}}}{{r}^{3}}$ |
7.A、B两球在光滑水平面上沿同一直线向同一方向运动,质量为1kg的A球动量是5kg•m/s,质量为7kg的B球的动量是7kg•m/s,当A球追上B球发生碰撞后,A、B两球的动量可能值为( )
| A. | PA=-5kg•m/s,PB=17kg•ms | B. | PA=6 kg•m/s,PB=6 kg•m/s | ||
| C. | PA=3 kg•m/s,PB=9 kg•m/s | D. | PA=-2 kg•m/s,PB=14 kg•m/s |
8.物体在水平恒力作用下,在水平面上由静止开始运动,当位移S0时撤去F,物体继续前进3S0后停止运动.若路面情况相同,则物体的摩擦力大小和最大动能是( )
| A. | f=$\frac{F}{4}$,Ek=$\frac{3}{4}$FS0 | B. | f=$\frac{F}{4}$,Ek=$\frac{1}{3}$FS0 | C. | f=$\frac{F}{3}$,Ek=FS0 | D. | f=$\frac{F}{3}$,Ek=4FS0 |
 如图,ab和cd是两条竖直放置的长直光滑金属导轨,MN和M'N'是两根用细线连接的金属杆,其质量分别为m和2m.竖直向上的外力F作用在杆MN上,使两杆水平静止,并刚好与导轨接触;两杆的总电阻为R,导轨间距为l.整个装置处在磁感应强度为B的匀强磁场中,磁场方向与导轨所在平面垂直.导轨电阻可忽略,重力加速度为g.在t=0时刻将细线烧断,保持F不变,金属杆和导轨始终接触良好.求
如图,ab和cd是两条竖直放置的长直光滑金属导轨,MN和M'N'是两根用细线连接的金属杆,其质量分别为m和2m.竖直向上的外力F作用在杆MN上,使两杆水平静止,并刚好与导轨接触;两杆的总电阻为R,导轨间距为l.整个装置处在磁感应强度为B的匀强磁场中,磁场方向与导轨所在平面垂直.导轨电阻可忽略,重力加速度为g.在t=0时刻将细线烧断,保持F不变,金属杆和导轨始终接触良好.求
