题目内容
在现代物理学的研究中,人们利用高能带电粒子轰击各种原子核,获得不同放射性同位素,为临床医学诊断和治疗提供了全新的高科技手段。高能带电粒子是由小型回旋加速器进行加速而获得,回旋加速器示意如图。其中置于高真空中的金属D形盒的半径为R,两盒间的距离为d,在左侧D形盒圆心处放有粒子源S,匀强磁场的磁感应强度为B,方向如图所示。带电粒子的质量为m,电荷量为q。设带电粒子从粒子源S进入加速电场时的初速度为零,带电粒子在加速器中运动总时间为t,其中忽略了带电粒子通过加速电场的运动时间,带电粒子在电场中的加速次数与回旋半圆周的个数相同,加速电场的电压大小可视为恒定、不计粒子重力。求: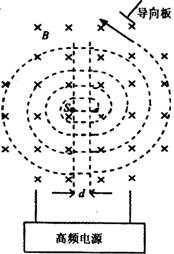
(1)此加速器所需的高频电源频率f和加速电压U。
(2)带电粒子在右侧D形盒中运动的相邻两个圆形轨道的半径之比。
解:(1)设带电粒子加速后最大速度为v,粒子在D形盒内受洛伦兹力作用做匀速圆周运动,由牛顿运动定律有qvB=m![]() ,粒子的回旋周期T=
,粒子的回旋周期T=![]() ,高频电源的频率f=
,高频电源的频率f=![]() ,粒子加速后的最大动能EK=
,粒子加速后的最大动能EK=![]() mv2,设粒子在电场中加速的次数为n,则EK=nqU 又t=n
mv2,设粒子在电场中加速的次数为n,则EK=nqU 又t=n![]() 联立以上各式解得U=
联立以上各式解得U=![]()
(2)设经过n次加速粒子获得速度vn,由动能定理得nqU=![]() (n=1,3,5,…),粒子再次进入右侧D形盒又经过两次加速有(n+2)qU=
(n=1,3,5,…),粒子再次进入右侧D形盒又经过两次加速有(n+2)qU=![]() ,第n次时qBvn=m
,第n次时qBvn=m![]() ,则Rn=
,则Rn=![]() ,第n+2次时qBv+2=m
,第n+2次时qBv+2=m![]() ,则Rn+2=
,则Rn+2=![]() ,联立可得
,联立可得![]() (n=1,3,5,…)
(n=1,3,5,…)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

