Question

【题目】如图所示，质量m=2.6kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动．（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：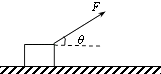

（1）金属块与地板间的动摩擦因数；
（2）若在运动过程的某一时刻保持力F的大小不变，突然将力的方向变为水平向右，这一时刻金属块的加速度大小为多少？
（3）若在匀速直线运动某一时刻撤去力F，金属块再经过多长时间停下来？

Answer 1

【答案】
（1）解：设地板对金属块的支持力为FN，金属块与地板的动摩擦因数为μ，因为金属块匀速运动，所以有：

Fcosθ=μFN

mg=Fsinθ+FN

解得：

答：金属块与地板间的动摩擦因数为0.4．

（2）解：由牛顿第二定律得：

F﹣μmg=ma1

代入数据解得：a1= m/s2≈﹣0.154m/s2

负号表示加速度方向与速度方向相反，大小为0.154m/s2

答：这一时刻金属块的加速度大小为0.154m/s2．

（3）解：撤去力F后有：μmg=ma2

代入数据有：a2=4m/s2

由t=

代入数据解得：t=1.25s．

答：金属块再经过1.25s停止．

【解析】因为物体做匀速运动，所以受力平衡，根据物体的平衡条件求解物体所受的摩擦力大小，根据竖直方向的力的平衡求解物体与水平面之间的压力，再根据滑动摩擦力的公式求动摩擦因数；撤去力F后，物体在摩擦力的作用下做匀减速运动，根据速度时间关系求出物体的运动时间。