题目内容
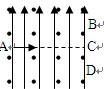
如图所示,空间存在着电场强度为E=2.5×102 N/C、方向竖直向上的匀强电场,一长为L=0.5m的绝缘细线,一端固定在O点,一端拴着质量m=0.5kg,电荷量∣q∣= 4×10-2 C的小球。现将细线拉直到水平位置,使小球由静止释放,则小球能运动到最高点.不计阻力。取g=10m/s2.求:

(1)小球的电性;
(2)细线在最高点受到的拉力T多大;
(3)若小球刚好运动到最高点时细线断裂,则细线断裂后小球继续运动到与O点水平方向距离为细线的长度L时,小球距O点的高度h。

(1)小球的电性;
(2)细线在最高点受到的拉力T多大;
(3)若小球刚好运动到最高点时细线断裂,则细线断裂后小球继续运动到与O点水平方向距离为细线的长度L时,小球距O点的高度h。
(1)正电 (2)15N (3)0.625m
试题分析:(1)由小球运动到最高点可知,小球带正电
(2)设小球运动到最高点时速度为v,对该过程由动能定理有:
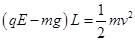 ①
① 在最高点对小球由牛顿第二定律得,
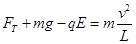 ②
② 由①②式解得,
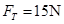
(3)小球在细线断裂后,在竖直方向的加速度设为a,则
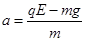 ③
③设小球在水平方向运动L的过程中,历时t,则
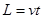 ④
④设竖直方向上的位移为s,则
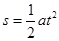 ⑤
⑤ 由①③④⑤解得,
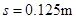
小球距O点高度为
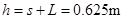 .
. 点评:小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂。从而可求出此时的速度,这是本题的突破口。值得注意是细线断裂后,速度与合力相垂直,且合力恒定,所以做类平抛运动。

练习册系列答案
相关题目
 ;
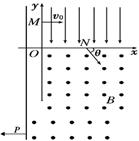
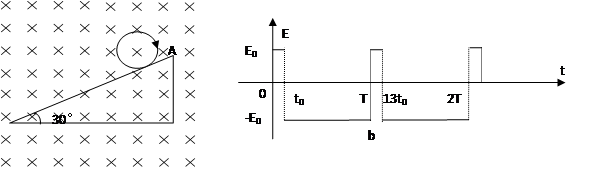
; )为K的带正电的粒子从第三象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场。不计粒子重力,求:
)为K的带正电的粒子从第三象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场。不计粒子重力,求: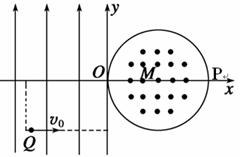
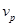 的大小
的大小
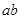 宽为
宽为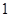 cm,
cm,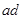 长为4cm,
长为4cm,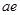 厚为
厚为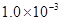 cm的导体,沿
cm的导体,沿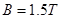 的匀强磁场垂直向里穿过
的匀强磁场垂直向里穿过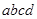 平面时,产生了
平面时,产生了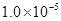 V的霍尔电压,(已知导体内定向移动的自由电荷是电子),则下列说法正确的是
V的霍尔电压,(已知导体内定向移动的自由电荷是电子),则下列说法正确的是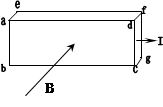
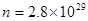 个
个
 ,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,
,匀强磁场的磁感应强度B=0.1T,方向垂直框架向上,现用1N的外力F由静止拉动ab杆,当ab的速度达到1m/s时,