Question

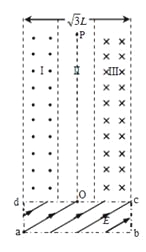
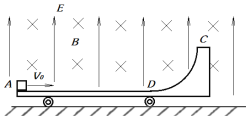
【题目】如图所示，质量M＝3.0kg的小车静止在光滑的水平地面上，AD部分是表面粗糙的水平导轨，DC部分是光滑的圆弧导轨，AD和DC部分平滑相连，整个导轨都是由绝缘材料制成的，小车所在空间内有竖直向上E＝40N/C的匀强电场和垂直纸面水平向里B＝2.0T的匀强磁场。今有一质量为m＝1.0kg带负电的滑块（可视为质点）以v0＝8m/s的水平速度向右冲上小车，当它过D点时对地速度为v1＝5m/s，对水平导轨的压力为10.5N，g取10m/s2。求：

（1）滑块的电量大小；

（2）滑块从A到D的过程中，小车、滑块系统损失的机械能；

（3）若滑块通过D时立即撤去磁场，求此后小车所能获得的最大速度。

Answer 1

【答案】（1）；（2）18J；（3）3m/s

【解析】

（1）在D点，竖直方向上满足：

解得：

（2）从A→D，滑块、小车系统水平方向动量守恒，设到D点时小车速度为u1，有：

解得：

由能量守恒定律可知系统损失的机械能为：

解得：

J

（3）撤去磁场后，滑块在圆弧轨道上运动的整个过程中，小车都在加速，因此滑块返回D点时，小车速度最大，设此时滑块、小车的速度分别为v2、u2，因滑块由D点上滑到滑回D点过程中，电场力做功为零，故系统在水平动量守恒的同时初末状态机械能相等，即：

mv0=mv2+Mu2

联立两式解得：

u2=1m/s（舍去）； u2=3m/s

即此后小车所能获得的最大速度为3m/s。