��Ŀ����
����Ŀ����ͼ��һ�ᵯ��ԭ��Ϊ2R����һ�˹̶������Ϊ370�Ĺ̶�ֱ���AC�ĵ�A������һ��λ��ֱ�����B�������ɴ�����Ȼ״̬������Ϊm��С���P��C���ɾ�ֹ��ʼ�»���AC=7R��P��ֱ�����Ķ�Ħ�������� =0.25���������ٶȴ�СΪg��(ȡsin37��=0.6,cos37��=0.8)
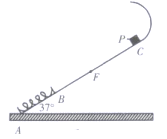
(1)��P��һ���˶���B��ʱ�ٶȵĴ�С��
(2)С���P��C���ɾ�ֹ��ʼ�»�����͵���E��(δ����)�����P�ع�������أ���ߵ㵽��F�㣬AF=4R����P�˶���E��ʱ���ɵĵ������ܣ�
(3)ֱ���AC��һ�뾶Ϊ![]() R�Ĺ⻬Բ�����������C�㣬б����Բ���������ͬһ��ֱ���ڡ��ı����P����������P����E�㣬�Ӿ�ֹ��ʼ�ͷš���֪P����Բ��������Կ�����Բ��������£���P������ȡֵ��Χ��
R�Ĺ⻬Բ�����������C�㣬б����Բ���������ͬһ��ֱ���ڡ��ı����P����������P����E�㣬�Ӿ�ֹ��ʼ�ͷš���֪P����Բ��������Կ�����Բ��������£���P������ȡֵ��Χ��
���𰸡���1��vB=2![]() ��2��W��=12mgR/5��3��
��2��W��=12mgR/5��3��![]()
��������(1)������C�˶���B�����ж��ܶ������ã�
![]()
��ã� ![]() ��
��
(2)�о�����C�˶���E����BE=x���˷���������W�������ݶ��ܶ�����ʽ��
![]()
�о�����E�˶���F����������W�������ݶ��ܶ�����ʽ��
![]()
��ã� ![]() ��
�� ![]() ��
��
(3) P����Բ��������Կ�����Բ��������£���P��Բ����Ӧ�䵽CD֮�䣬��ͼ��C��D��������ٽ�㡣
�о�����E�˶���C����ı���������������Ϊm1�����ݶ��ܶ�����ʽ��
![]()
�о�����E�˶���D����CD����߶Ȳ�Ϊh����������Ϊm2�����ݶ��ܶ�����ʽ��
![]()
�ɼ��ι�ϵ�ã� ![]() ,����
,����![]()
�����ϸ�ʽ������ã� ![]() ��
�� ![]()
�����������ȡֵ��ΧΪ�� ![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�