题目内容
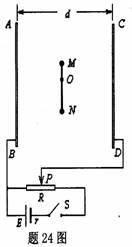
如题24图所示，电源电动势为E，内阻为r，滑动变阻器全电阻为R，且R=3r．间距为d的两平行金属板AB、CD竖直放置，闭合开关S，板间电场视为匀强电场．板间有一长为L的绝缘细轻杆，杆能绕水平固定转轴O在竖直面内无摩擦转动，杆上端固定质量为m带电量为+q的金属小球M，杆下端固定质量为2m带电量为-q的金属小球N，已知ON=2OM，并且
，两带电小球可视为点电荷，不影响匀强电场的分布，两电荷间相互作用力不计，取重力加速度为g。现调节滑片P使其处于滑动变阻器中点，闭合电键S，待电场稳定后讨论以下问题。求：
（1）两板间电压U
（2）若将绝缘细轻杆从图示竖直位置由静止开始释放，轻杆将绕转轴O顺时针转动，试求小球M运动的最大速度．（用g、L表示）
解：（1）设通过电源的电流强度为I，由闭合电路的欧姆定律得：
（2分）
两板间电压：有
（2分） 解得：
（2分）
（2）设轻杆绕转轴O顺时针转过
时,小球M获得最大速度, 同时小球N获得最大速度
,由二者运动角速度关系：
得：（4分）
设平行金属板间电场强度大小为，由能量守恒得：
（4分）
可解得：
（4分）
练习册系列答案
相关题目
