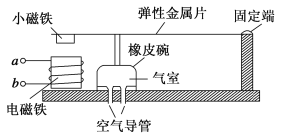
题目内容
【题目】如图所示,一小车静止在水平面上,其天花板上的O点悬挂一根串联着不同质量的A、B两小球的细绳,其中M>m。若小车沿水平面以加速度a向右加速运动,问稳定后OA绳、AB绳与竖直方向的夹角分别为多大?(小球不会碰到车壁)

【答案】arctan![]() arctan
arctan![]()
【解析】试题分析:以小球A为研究对象,受力分析根据竖直方向的平衡和水平方向的牛顿第二定律,结合即可求出OA绳与竖直方向的夹角,同理可求出AB绳与竖直方向的夹角。
设两绳与竖直方向的夹角分别为θA和θB。以两球整体为对象,受力如图:

根据竖直方向的平衡和水平方向的牛顿第二定律有:
FAcosθA=(M+m)g
FAsinθA=(M+m)a
解得:tanθA=![]() 即θA=arctan
即θA=arctan![]() 。
。
以B球为对象,受力如图:

根据竖直方向的平衡和水平方向的牛顿第二定律有:
FBcosθB=mg
FBsinθB=ma
解得:tanθB=![]() 即:θB=arctan
即:θB=arctan![]() 。
。

练习册系列答案
相关题目