题目内容
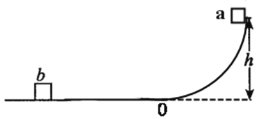
【题目】如图所示,光滑的轨道固定在竖直平面内,其O点左边为光滑的水平轨道,O点右边为四分之一圆弧轨道,高度h=0.8m,左右两段轨道在O点平滑连接。质量m=0.1kg的小滑块a由静止开始从圆弧轨道的顶端沿轨道下滑,到达水平段后与处于静止的小滑块b发生碰撞,小滑块b的质量M=0.4kg,碰撞后小滑块a恰好停止运动。取重力加速度g=10m/s2,求
(1)小滑块a通过O点时对轨道的压力的大小和方向;
(2)碰撞瞬间小滑块b所受冲量的大小;
(3)碰撞过程中小滑块a、b组成的系统损失的机械能。
【答案】(1)3N,方向竖直向下;(2)0.4 N·s;(3)0.6J
【解析】
(1)小滑块从曲线轨道上下滑的过程中,由动能定理得:
![]()
代入数据解得,小滑块a通过O点时的速度:
v0=4m/s
a通过O点时
![]()
代入数据解得,小滑块a通过O点时所受支持力为
N=3N
根据牛顿第三定律,小滑块对轨道的压力为3N;方向竖直向下;
(2)碰撞过程系统动量守恒,以向左为正方向,由动量守恒定律得:
mv0=Mv1
滑块b所受冲量的大小,由冲量定理得:
I=Mv1
代入数据计算
I=0.4N·s
(3)碰撞过程中小滑块a、b组成的系统损失的机械能:
ΔE=![]() mv02﹣
mv02﹣![]() Mv12
Mv12
代入数据解得
ΔE=0.6J

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目