题目内容
8.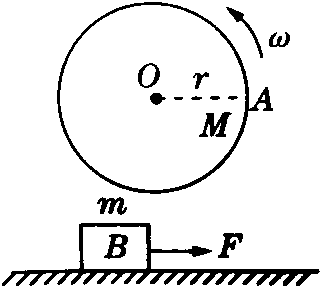 如图所示,B物体放在光滑的水平地面上,在水平力F的作用由静止开始运动,B物体的质量为m,同时A物体在竖直面内由M点开始做半径为r、角速度为ω的匀速圆周运动.求满足使A、B速度存在相同的情况时力F的取值.
如图所示,B物体放在光滑的水平地面上,在水平力F的作用由静止开始运动,B物体的质量为m,同时A物体在竖直面内由M点开始做半径为r、角速度为ω的匀速圆周运动.求满足使A、B速度存在相同的情况时力F的取值.
分析 A、B速度相同,包括速度大小和方向都相同,而B的速度水平向右,则A一定在最低点才有可能速度与B相同,根据牛顿第二定律结合运动学基本公式求解.
解答 解:A在最低点时,速度的大小和方向才可能与B相同,
A的速度大小vA=ωr,周期T=$\frac{2π}{ω}$,A从图示位置运动到最低点的时间t=nT+$\frac{3}{4}T$=$\frac{2π(n+\frac{3}{4})}{ω}$,(n=0,1,2…)
B做匀加速直线运动,加速度a=$\frac{F}{m}$,运动的时间t=$\frac{2π(n+\frac{3}{4})}{ω}$,(n=0,1,2…)
则有:vB=vA=at
解得:F=$\frac{m{ω}^{2}r}{2π(n+\frac{3}{4})}$,(n=0,1,2…)
答:满足使A、B速度存在相同的情况时力F的取值为$\frac{m{ω}^{2}r}{2π(n+\frac{3}{4})}$,(n=0,1,2…).
点评 本题主要考查了匀速圆周运动基本公式、牛顿第二定律以及匀加速直线运动速度时间公式的直接应用,知道只有A在最低点AB的速度才可能相同,特别注意圆周运动具有周期性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.一辆红旗牌汽车启动时,速度达到100km/h用时20s,而一列火车达到这个速度大约要用500s,则在启动过程中( )
| A. | 汽车速度变化比火车大 | B. | 汽车速度变化比火车快 | ||
| C. | 两车的速度变化一样大 | D. | 火车运行的速度一定比汽车大 |
19. 如图所示,斜面体置于粗糙水平面上,斜面光滑.小球被轻质细线系住放在斜面上,细线另一端跨过光滑定滑轮,用力拉细线使小球沿斜面缓慢下移一段距离,斜面体始终静止.移动过程中( )
如图所示,斜面体置于粗糙水平面上,斜面光滑.小球被轻质细线系住放在斜面上,细线另一端跨过光滑定滑轮,用力拉细线使小球沿斜面缓慢下移一段距离,斜面体始终静止.移动过程中( )
 如图所示,斜面体置于粗糙水平面上,斜面光滑.小球被轻质细线系住放在斜面上,细线另一端跨过光滑定滑轮,用力拉细线使小球沿斜面缓慢下移一段距离,斜面体始终静止.移动过程中( )
如图所示,斜面体置于粗糙水平面上,斜面光滑.小球被轻质细线系住放在斜面上,细线另一端跨过光滑定滑轮,用力拉细线使小球沿斜面缓慢下移一段距离,斜面体始终静止.移动过程中( )| A. | 细线对小球的拉力变大 | B. | 斜面对小球的支持力变大 | ||
| C. | 斜面体对地面的压力变大 | D. | 地面对斜面体的摩擦力变大 |
13.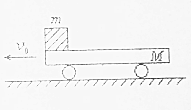 如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )
如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )
 如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )
如图所示,在光滑的水平地面上,质量为M、足够长的小平板车以速度v向左匀速运动,一质量为m的物块被无初速度地放到车的左端,由于摩擦力的作用,物块也运动起来,已知动摩擦因数为μ,当物块达到最大速度时( )| A. | 平板车的速度最小 | |
| B. | 此过程中M和m组成的系统所受摩擦力冲量为零 | |
| C. | 此过程中摩擦力对系统做功为零 | |
| D. | 经历此过程后,m所受合外力的冲量为零 |
20. 如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )
如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )
 如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )
如图甲,某电场的一条电场线与Ox轴重合,电场中x坐标上电势随位置x变化的图象如图乙所示(曲线的斜率为电场强度大小),如果有一电荷在x2处由静止释放,电荷仅受电场力的作用,则电荷运动到坐标原点的过程中( )| A. | 加速度越来越小 | B. | 电势能越来越大 | ||
| C. | 动能先增大后减小 | D. | 电场力做功的功率越来越大 |
16.质点作直线运动的v-t图象如图所示,则( )
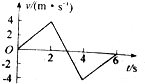

| A. | 6s内物体运动的平均速率为零 | |
| B. | 6s内物体运动的平均速度为零 | |
| C. | 2-4s内的位移为零,路程为4m | |
| D. | 0-2s内的加速度为4-6s内的加速度方向相反,大小相等 |
17.下列说法正确的是( )
| A. | 天然放射现象的发现揭示了原子核有复杂的结构 | |
| B. | α射线、β射线和γ射线是三种波长不同的电磁波 | |
| C. | 在光电效应实验中,用同种频率的光照射不同的金属表面,从金属表面逸出的光电子的最大初动能Ek越大,则这种金属的逸出功W0越小 | |
| D. | 放射性元素的半衰期不随温度和压强的变化而变化 | |
| E. | 比结合能越大表示原子核中核子结合得越松散,原子核越不稳定 |
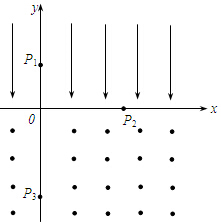 如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速度为v0,方向沿x轴正方向;然后,经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点.不计重力.求:
如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速度为v0,方向沿x轴正方向;然后,经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点.不计重力.求: 知滑块重力G=10N,与水平方向夹角θ=37°大小为10N的压力F作用在物块上.
知滑块重力G=10N,与水平方向夹角θ=37°大小为10N的压力F作用在物块上.