题目内容
将质量为0.2kg的一物体由地面竖直向上抛出,空气阻力不计,上升到最高点后又下落到离地高30m时速度大小变为25m/s,以地面为零势能面,求:
(1)此时物体的机械能,
(2)物体抛出时速度的大小,
(3)物体能上升的最大高度,
(4)以向上为正方向,画出物体从抛出到此时的位移的图示.
(1)此时物体的机械能,
(2)物体抛出时速度的大小,
(3)物体能上升的最大高度,
(4)以向上为正方向,画出物体从抛出到此时的位移的图示.
分析:(1)机械能包括动能和重力势能,根据定义式列式求解;
(2)根据机械能守恒定律列式求解物体抛出时速度的大小;
(3)根据机械能守恒定律列式求解物体能上升的最大高度;
(4)先求解位移表达式,再画图,标出关键点坐标.
(2)根据机械能守恒定律列式求解物体抛出时速度的大小;
(3)根据机械能守恒定律列式求解物体能上升的最大高度;
(4)先求解位移表达式,再画图,标出关键点坐标.
解答:解:(1)物体的动能为:Ek1=
mv2=
×0.2×252J=62.5J;
物体的重力势能为:Ep1=mgh=0.2×10×30J=60J;
故机械能为:E=Ek1+EP1=122.5J;
(2)由于只有重力做功,运动过程中机械能守恒,根据机械能守恒定律,有:
m
=E
解得:v0=
=
≈35m/s
(3)由于只有重力做功,运动过程中机械能守恒,根据机械能守恒定律,有:
mgH=E
解得:H=
=
m=61.25m;
(4)物体的位移:x=v0t-
gt2=35t-5t2;
作出x-t图象,如图所示:
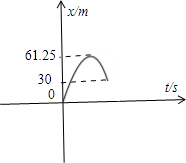
答:(1)此时物体的机械能为122.5J;
(2)物体抛出时速度的大小为35m/s;
(3)物体能上升的最大高度为61.25m;
(4)如图所示.
| 1 |
| 2 |
| 1 |
| 2 |
物体的重力势能为:Ep1=mgh=0.2×10×30J=60J;
故机械能为:E=Ek1+EP1=122.5J;
(2)由于只有重力做功,运动过程中机械能守恒,根据机械能守恒定律,有:
| 1 |
| 2 |
| v | 2 0 |
解得:v0=
|
|
(3)由于只有重力做功,运动过程中机械能守恒,根据机械能守恒定律,有:
mgH=E
解得:H=
| E |
| mg |
| 122.5 |
| 0.2×10 |
(4)物体的位移:x=v0t-
| 1 |
| 2 |
作出x-t图象,如图所示:

答:(1)此时物体的机械能为122.5J;
(2)物体抛出时速度的大小为35m/s;
(3)物体能上升的最大高度为61.25m;
(4)如图所示.
点评:本题关键是明确物体的运动规律,然后选择恰当的运动学公式列式求解,不难.

练习册系列答案
相关题目