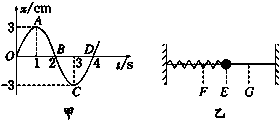题目内容
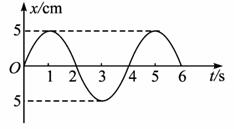
图1为一弹簧振子的示意图，弹簧的劲度系数k=40N/m，小球的质量m=0.1kg，O为平衡位置，B、C为小球离开O点的最远位置．取向右为正方向，从弹簧振子向右经过平衡位置开始计时，图2为它的振动图象．已知，当弹簧形变量为x时，弹簧的弹性势能为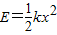
．在运动过程中（ ）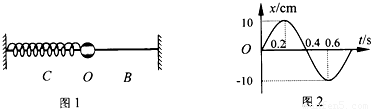
A．小球离开平衡位置的最大距离为10 cm
B．小球最大加速度为80 m/s2
C．在t=0.2 s时，小球的弹性势能为0.2 J
D．小球离开平衡位置的距离为5 cm时，速度大小为
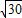m/s
【答案】分析：从图2得到振动的幅度，然后胡克定律和牛顿第二定律列式求解加速度，根据机械能守恒定律求解任意位置的速度．
解答：解：A、从图2得到振动的幅度为10cm，故A正确；
B、小球最大加速度为：a=-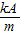
=-
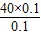=-40m/s2，故B错误；
C、在t=0.2 s时，小球的弹性势能为：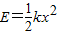
=
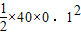=0.2J，故C正确；
D、根据机械能守恒定律，有：E=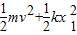
，解得：v=
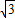m/s，故D错误；
故选AC．
点评：本题关键明确水平方向的弹簧振子运动过程中，系统机械能守恒，基础题．
解答：解：A、从图2得到振动的幅度为10cm，故A正确；
B、小球最大加速度为：a=-
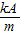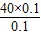=-=-40m/s2，故B错误；C、在t=0.2 s时，小球的弹性势能为：
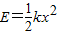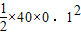==0.2J，故C正确；D、根据机械能守恒定律，有：E=
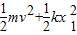，解得：v=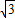m/s，故D错误；故选AC．
点评：本题关键明确水平方向的弹簧振子运动过程中，系统机械能守恒，基础题．
练习册系列答案
相关题目
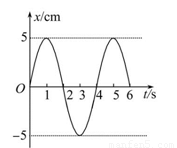
如图所示为一弹簧振子的振动图象，弹簧的精度系数为k=100N/m，振子的质量m=0.5kg试完成以下问题：
