Question

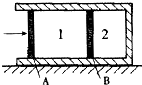
一横截面积为S的气缸水平放置，固定不动，两个活塞A和B将气缸分隔为1、2两气室，温度均为27℃，达到平衡时1、2两气室长度分别为30cm和20cm，如图所示．在保持两气室温度不变的条件下，缓慢推动活塞A，使之向右移动5cm，不计活塞与气缸壁之间的摩擦，大气压强为1.0×10⁵Pa．求：
（1）活塞B向右移动的距离与气室2中气体的压强．
（2）若将活塞A用销子固定，保持气室1的温度不变，要使气室2中气体的体积恢复原来的大小，则应将气室2气温度升高为多少℃？

Answer 1

【答案】分析：1、由题，温度保持不变，封闭在气缸中的气体发生等温变化，根据玻意耳定律，分别对气室1和气室2列方程，由这两方程可解得活塞B向右移动的距离与气室2中气体的压强；
2、对气室2内气体运用查理定律=．对气室1内气体运用玻意耳定律p L₁ S=p′（L₁-d）S，代入数据计算，可解得T₂，再转换成摄氏度即可．
解答：解：（1）因气缸水平放置，又不计活塞的摩擦，故平衡时两气室内的压强必相等，均为P．设在活塞A向右移动d的过程中活塞B向右移动的距离为x，平衡时两气缸内压强均为P，因温度不变，根据玻意耳定律，得
气室1    pL₁ S=p（L₁-d+x）S------①
气室2    pL₂ S=p （L₂-x） S-------②
由上面①②两式解得
x==×5cm=2 cm 
将  x=2 cm代②式，得   
p==1.1×10⁵Pa 
（2）活塞A固定，气室2中气体的体积恢复为 L₂S 时，温度升高为T₂，压强增大为 p′，此过程为等容过程，运用查理定律．
=   
这时气室1中气体的体积为（L₁-d）S，压强增大为 p′，温度仍为27℃，为等温过程，根据玻意耳定律，得
p L₁ S=p′（L₁-d）S 
解方程组得   T₂=T₁=×300=360 K
t₂=360 K-273 K=87℃
答：（1）活塞B向右移动的距离为2cm，气室2中气体的压强为1.1×10⁵Pa．
（2）若将活塞A用销子固定，保持气室1的温度不变，要使气室2中气体的体积恢复原来的大小，则应将气室2气温度升高为87℃．
点评：本题关键要确定气体发生何种状态变化，再选择合适的规律列式求解．难度不大，计算要小心，容易出错．