题目内容
(25分)从赤道上的C点发射洲际导弹,使之精确地击中北极点N,要求发射所用的能量最少.假定地球是一质量均匀分布的半径为R的球体,R=6400km.已知质量为m的物体在地球引力作用下作椭圆运动时,其能量E与椭圆半长轴a的关系为![]() 式中M为地球质量,G为引力常量.
式中M为地球质量,G为引力常量.

1.假定地球没有自转,求最小发射速度的大小和方向(用速度方向与从地心O到发射点C的连线之间的夹角表示).
2.若考虑地球的自转,则最小发射速度的大小为多少?
3.试导出![]() 。
。
解析:
1.这是一个大尺度运动,导弹发射后,在地球引力作用下将沿椭圆轨道运动.如果导弹能打到N点,则此椭圆一定位于过地心O、北极点N和赤道上的发射点C组成的平面(此平面是C点所在的子午面)内,因此导弹的发射速度(初速度v)必须也在此平面内,地心O是椭圆的一个焦点.根据对称性,注意到椭圆上的C、N两点到焦点O的距离相等,故所考察椭圆的长轴是过O点垂直CN的直线,即图上的直线AB,椭圆的另一焦点必在AB上.已知质量为m的物体在质量为M的地球的引力作用下作椭圆运动时,物体和地球构成的系统的能量E(无穷远作为引力势能的零点)与椭圆半长轴a的关系为![]() (1)
(1)
要求发射的能量最少,即要求椭圆的半长轴a最短.根据椭圆的几何性质可知,椭圆的两焦点到椭圆上任一点的距离之和为2a,现C点到一个焦点O的距离是定值,等于地球的半径R,只要位于长轴上的另一焦点到C的距离最小,该椭圆的半长轴就最小.显然,当另一焦点位于C到AB的垂线的垂足处时,C到该焦点的距离必最小.由几何关系可知
![]() (2)
(2)
设发射时导弹的速度为v,则有
![]() (3)
(3)
解(1)、(2)、(3)式得![]() (4)
(4)
因![]() (5)
(5)
比较(4)、(5)两式得![]() (6)
(6)
代入有关数据得v=7.2km/s (7)
速度的方向在C点与椭圆轨道相切.根据解析几何知识,过椭圆上一点的切线的垂直线,平分两焦点到该点连线的夹角∠OCP.从图中可看出,速度方向与OC的夹角
![]() (8)
(8)
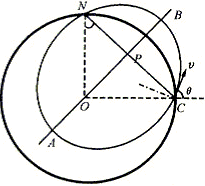
2.由于地球绕通过ON的轴自转,在赤道上C点相对地心的速度为![]() (9)
(9)
式中R是地球的半径,T为地球自转的周期,T=24×3600s=86400s,故
vC=0.46km/s(10)
C点速度的方向垂直于子午面(图中纸面).位于赤道上C点的导弹发射前也有与子午面垂直的速度vC,为使导弹相对于地心速度位于子午面内,且满足(7)、(8)两式的要求,导弹相对于地面(C点)的发射速度应有一大小等于vC、方向与vC相反的分速度,以使导弹在此方向相对于地心的速度为零,导弹的速度的大小为
![]() (11)
(11)
代入有关数据得v′=7.4km/s (12)
它在赤道面内的分速度与vC相反,它在子午面内的分速度满足(7)、(8)两式.
3.质量为m的质点在地球引力作用下的运动服从机械能守恒定律和开普勒定律,故对于近地点和远地点有下列关系式
![]() (13)
(13)
![]() (14)
(14)
式中v1、v2分别为物体在远地点和近地点的速度,r1、r2为远地点和近地点到地心的距离.将(14)式中的v1代入(13)式,经整理得
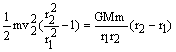 (15)
(15)
注意到r1+r2=2a (16)
得![]() (17)
(17)
因![]() (18)
(18)
由(16)、(17)、(18)式得![]() (19)
(19)
评分标准:(本题25分)
1.14分.(2)式6分,(3)式2分,(6)、(7)式共4分,(8)式2分.
2.6分.(11)式4分,(12)式2分.
3.5分.(13)、(14)式各1分,(19)式3分.
