题目内容
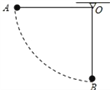
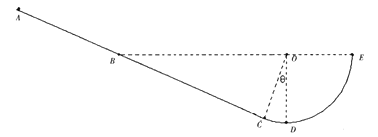
【题目】如图所示,ABCDE为固定在竖直平面内的轨道,ABC为直轨道,AB光滑,BC粗糙,CDE为光滑圆弧轨道,轨道半径为R,∠COD=θ(θ<5°),直轨道与圆弧轨道相切于C点,其中圆心O与BE、C’与C均处于同一水平面上,OD竖直。现有一质量为m的小物体(可以看作质点)从斜面上的A点静止滑下,小物体与BC间的动摩擦因数为![]() ,现要使小物体第一次滑入圆弧轨道后即恰好在C和C’间做简谐运动(重力加速度为g)。求:
,现要使小物体第一次滑入圆弧轨道后即恰好在C和C’间做简谐运动(重力加速度为g)。求:
(1)小物体过D点时对轨道的压力大小。
(2)直轨道AB部分的长度S。
【答案】(1)![]() (2)
(2)![]()
【解析】(1)小物体下滑到C点速度为零才能第一次滑入圆弧轨道即恰好做简谐运动。
从C到D由机械能守恒定律有:![]()
在D点根据牛顿第二定律得:![]()
根据牛顿第三定律得:![]()
解以上方程可得: ![]()
(2)从A到C由动能定理有:![]()
解方程得: ![]()

练习册系列答案
相关题目