题目内容
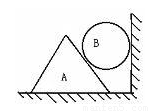
如图所示，光滑的金属球B放在横截面为等边三角形的物体A与竖直墙之间，恰好匀速下滑，已知物体A的重力是B重力的6倍，不计球跟斜面和墙之间的摩擦，问：物体A与水平面之间的动摩擦因数是多少？
解：对球受力分析，受重力、墙壁的支持力和三角形物体的支持力，如图所示：
根据平衡条件，有：
N1=2mg；
再对三角形物体受力分析，受重力、球的压力、支持力和向右的滑动摩擦力，如图所示：
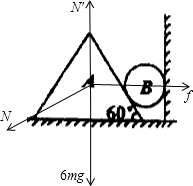
竖直方向受力平衡，有：
竖直方向：6mg+Nsin30°=N′
水平方向：Nsin60°=f
根据滑动摩擦定律，有：
f=μN′
解得：N′=7mg
μ=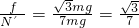
答：物体A与水平面之间的动摩擦因数是
．
分析：球斜面均做匀速运动，受力平衡；对球受力分析，受重力、墙壁的支持力和三角形物体的支持力，根据平衡条件求解出三角形物体的支持力；再分析三角形物体，受重力、球对其的压力、支持力和滑动摩擦力，受力平衡，结合滑动摩擦定律求解滑动摩擦力．
点评：本题关键是先后对两个物体受力分析，然后根据共点力平衡条件列式，最后再根据滑动摩擦定律求解动摩擦因素．
根据平衡条件，有：
N1=2mg；
再对三角形物体受力分析，受重力、球的压力、支持力和向右的滑动摩擦力，如图所示：
竖直方向受力平衡，有：
竖直方向：6mg+Nsin30°=N′
水平方向：Nsin60°=f
根据滑动摩擦定律，有：
f=μN′
解得：N′=7mg
μ=
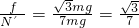
答：物体A与水平面之间的动摩擦因数是
．分析：球斜面均做匀速运动，受力平衡；对球受力分析，受重力、墙壁的支持力和三角形物体的支持力，根据平衡条件求解出三角形物体的支持力；再分析三角形物体，受重力、球对其的压力、支持力和滑动摩擦力，受力平衡，结合滑动摩擦定律求解滑动摩擦力．
点评：本题关键是先后对两个物体受力分析，然后根据共点力平衡条件列式，最后再根据滑动摩擦定律求解动摩擦因素．
练习册系列答案
通城学典默写能手系列答案
相关题目
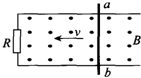如图所示，光滑的金属导轨放在磁感应强度B=0.2T的匀强磁场中．平行导轨的宽度d=0.3m，定值电阻R=0.5Ω．在外力F作用下，导体棒ab以v=20m/s的速度沿着导轨向左匀速运动．导体棒和导轨的电阻不计．求：
如图所示，光滑的金属球B放在横截面为等边三角形的物体A与竖直墙之间，恰好匀速下滑，已知物体A的重力是B重力的6倍，不计球跟斜面和墙之间的摩擦，问：物体A与水平面之间的动摩擦因数是多少？
如图所示，光滑的金属导轨间距为L，导轨平面与水平面成α角，导轨下端接有阻值为R的电阻，质量为m的金属细杆ab与绝缘轻质弹簧相连静止在导轨上，弹簧劲度系数为k，上端固定，弹簧与导轨平面平行，整个装置处在垂直于导轨平面斜向上的匀强磁场中，磁感应强度为B．现给杆一沿轨道向下的初速度v0，杆向下运动至速度为零后，再沿轨道平面向上运动达最大速度，大小为v1，然后减速为零，再沿轨道平面向下运动…一直往复运动到静止（导轨与金属杆的电阻忽略不计）．试求：
