题目内容
7.一个质点在平衡位置O点附近做简谐运动,若从经过O点开始计时,t=3s时第一次经过某点,再继续运动,又经过2s它第二次经过该点,则质点第三次经过该点还需要时间( )| A. | 8s | B. | 4s | C. | 14s | D. | $\frac{10}{3}$s |
分析 分析质点可能的运动情况,画出运动轨迹,确定周期,即一次全振动所用的时间,再确定经过多长时间质点第三次经过P点.
解答  解:如图所示,设质点B、C之间振动
解:如图所示,设质点B、C之间振动
若质点先向左开始振动,画出其振动一个周期内运动轨迹,如图1所示,则知周期T1=3s+2s+$\frac{1}{3}$s=$\frac{16}{3}$s,则该质点再时间△t1=T-2s=$\frac{10}{3}$s,经第三次经过M点.
若质点先向右开始振动,画出其振动一个周期内运动轨迹,如图2所示,则知周期T1=4(3s+$\frac{1}{2}$×2s)=16s,则该质点再时间△t2=T-2s=14s,经第三次经过M点.故AB错误,CD正确.
故选:CD.
点评 本题关键画出质点的运动轨迹,分析时间与周期的关系,一定注意振动方向的不定性,据此分类分析振动方向.

练习册系列答案
相关题目
2. 宇宙中两颗靠得比较近的恒星只受到彼此之间的万有引力作用互相绕转,称之为双星系统,如图所示,双星A、B绕其连线上的O点做匀速圆周运动,已知A、B恒星的半径之比为m,A、B做圆周运动的轨道半径之比为n.则( )
宇宙中两颗靠得比较近的恒星只受到彼此之间的万有引力作用互相绕转,称之为双星系统,如图所示,双星A、B绕其连线上的O点做匀速圆周运动,已知A、B恒星的半径之比为m,A、B做圆周运动的轨道半径之比为n.则( )
 宇宙中两颗靠得比较近的恒星只受到彼此之间的万有引力作用互相绕转,称之为双星系统,如图所示,双星A、B绕其连线上的O点做匀速圆周运动,已知A、B恒星的半径之比为m,A、B做圆周运动的轨道半径之比为n.则( )
宇宙中两颗靠得比较近的恒星只受到彼此之间的万有引力作用互相绕转,称之为双星系统,如图所示,双星A、B绕其连线上的O点做匀速圆周运动,已知A、B恒星的半径之比为m,A、B做圆周运动的轨道半径之比为n.则( )| A. | A、B两恒星表面的重力加速度之比为$\frac{1}{m}$ | |
| B. | A、B两恒星表面的重力加速度之比为$\frac{1}{nm}$ | |
| C. | A、B两恒星的密度之比为$\frac{1}{{m}^{3}}$ | |
| D. | A、B两恒星的密度之比为$\frac{1}{n{m}^{3}}$ |
12.关于平抛运动,下列说法错误的是( )
| A. | 平抛物体在运动过程中,其加速度和水平速度保持不变 | |
| B. | 平抛物体可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动 | |
| C. | 平抛物体是做曲线运动的,因此它不可能是匀变速运动 | |
| D. | 平抛物体水平飞行的距离与初速度和高度有关有关 |
16. 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )
 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时( )| A. | 人拉绳行走的速度为$\frac{v}{cosθ}$ | B. | 人拉绳行走的速度为vcosθ | ||
| C. | 船的加速度为$\frac{Tcosθ-f}{m}$ | D. | 船的加速度为$\frac{T-f}{m}$ |


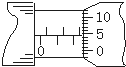 测一小球直径时,螺旋测微器的示数如图所示,可知该小球的直径为2.545mm,若将可动刻度顺时针转过72°(从右往左看),则读数为2.445mm.
测一小球直径时,螺旋测微器的示数如图所示,可知该小球的直径为2.545mm,若将可动刻度顺时针转过72°(从右往左看),则读数为2.445mm. 如图电路,开关原先闭合,电路处于稳定,在某一时刻突然断开开关S,则通过电阻R 1中的电流I1随时间变化的图线可能是下图中的( )
如图电路,开关原先闭合,电路处于稳定,在某一时刻突然断开开关S,则通过电阻R 1中的电流I1随时间变化的图线可能是下图中的( )



 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球沿垂直球网的方向击出.已知底线到网的距离为L,重力加速度取g,将球的运动视作平抛运动,求:
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球沿垂直球网的方向击出.已知底线到网的距离为L,重力加速度取g,将球的运动视作平抛运动,求: