题目内容
20. 如图所示,一种特殊薄材料的隔离层与y轴重合,xOy平面中,x<0的区域内有匀强电场,场强大小为E,方向沿x轴正向;x>0的区域内有匀强磁场,磁感应强度大小为B,方向垂直纸面向外.一光滑绝缘材料制成的半圆形轨道固定在y轴右侧,半径为R,圆M坐标为(R、O),直径OQ在x轴上;一电荷量为+q,质量为m的微粒(不计重力)从x轴负半轴某处静止释放,经电场加速后通过隔离层,从O点沿X轴正向进入磁场,垂直打在P点,MP与竖直方向MN夹角α=30°,已知微粒与轨道碰撞过程时间极短可忽略不计,碰撞前后微粒电荷量及速度大小保持不变,速度方向与碰撞前相反.
如图所示,一种特殊薄材料的隔离层与y轴重合,xOy平面中,x<0的区域内有匀强电场,场强大小为E,方向沿x轴正向;x>0的区域内有匀强磁场,磁感应强度大小为B,方向垂直纸面向外.一光滑绝缘材料制成的半圆形轨道固定在y轴右侧,半径为R,圆M坐标为(R、O),直径OQ在x轴上;一电荷量为+q,质量为m的微粒(不计重力)从x轴负半轴某处静止释放,经电场加速后通过隔离层,从O点沿X轴正向进入磁场,垂直打在P点,MP与竖直方向MN夹角α=30°,已知微粒与轨道碰撞过程时间极短可忽略不计,碰撞前后微粒电荷量及速度大小保持不变,速度方向与碰撞前相反.(已知当|x|<1,且当n→∞时,xn=0)求:
(1)若不计微粒穿过隔离层的能量损失,则该微粒释放的坐标;
(2)该微粒第一次在磁场中运动的时间;
(3)若每次微粒穿过隔离层动能损失l0%,则该微粒最终停在何处.
分析 (1)微粒在电场中加速,在磁场中做匀速圆周运动,应用动能定理与牛顿第二定律求出微粒的轨道半径,然后求出微粒释放位置的坐标.
(2)求出微粒在磁场中做圆周运动的周期,根据微粒在磁场中转过的圆心角求出微粒的运动时间.
(3)分析清楚微粒的运动过程,求出微粒做圆周运动的轨道半径,然后求出微粒静止位置的坐标.
解答 解:(1)微粒在电场中加速,由动能定理得:qEx=$\frac{1}{2}$mv2-0,
微粒在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,由题意可知:r=2Rcos30°=$\sqrt{3}$R,
解得:x=$\frac{3q{B}^{2}{R}^{2}}{2mE}$,坐标为:(-$\frac{3q{B}^{2}{R}^{2}}{2mE}$,0);
(2)微粒每次与轨道碰撞后等速率反弹,微粒运动轨迹如图所示:
微粒在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,
微粒第一次在磁场中运动的时间:t=$\frac{3}{2}$T=$\frac{3πm}{qB}$;
(3)微粒前一次出磁场的动能EK与下一次进磁场的动能间的关系:EK′=$\frac{81}{100}$EK,
微粒做圆周运动的轨道半径是前一次在磁场中做圆周运动半径的:$\frac{9}{10}$,
轨道半径成等比递减,最后离子停在y轴上,
y=2r+2r•$\frac{9}{10}$+2r•($\frac{9}{10}$)2+2r•($\frac{9}{10}$)3+…=20$\sqrt{3}$R,
则微粒停止位置的坐标为:(0,-20$\sqrt{3}$R);
答:(1)若不计微粒穿过隔离层的能量损失,则该微粒释放的坐标为:(-$\frac{3q{B}^{2}{R}^{2}}{2mE}$,0);
(2)该微粒第一次在磁场中运动的时间为:$\frac{3πm}{qB}$;
(3)若每次微粒穿过隔离层动能损失l0%,该微粒最终停止位置的坐标为:(0,-20$\sqrt{3}$R).
点评 本题考查了带电微粒在电场与磁场中的运动,分析清楚微粒的运动过程是正确解题的关键,作出微粒的运动轨迹,应用动能定理与牛顿第二定律、粒子做圆周运动的周期公式可以解题;解题时注意数学归纳法、等比数列求和公式的应用.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 如图所示,一质量为M的斜面静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且质量均为m,则( )
如图所示,一质量为M的斜面静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且质量均为m,则( )| A. | A、B保持相对静止 | |
| B. | 地面对斜面体的摩擦力等于mg(sinθ-μcosθ)cosθ+Fcosθ | |
| C. | 地面受到的压力等于(M+2m)g | |
| D. | B与斜面间动摩擦因数为$\frac{F-mgsinθ-μmgcosθ}{2mgcosθ}$ |
| A. | “月亮女神”的线速度大于“嫦娥一号”的线速度 | |
| B. | “月亮女神”的向心加速度小于“嫦娥一号”的向心加速度 | |
| C. | “月亮女神”的周期大于“嫦娥一号”的周期 | |
| D. | “月亮女神”的角速度小于“嫦娥一号”的角速度 |
 如图所示,电源电动势E=6V,内阻不计,电阻R1=2Ω,R2=4Ω,电容C1=2μF,C2=3μF,则当电键S断开后,通过R2的电荷量为( )
如图所示,电源电动势E=6V,内阻不计,电阻R1=2Ω,R2=4Ω,电容C1=2μF,C2=3μF,则当电键S断开后,通过R2的电荷量为( )| A. | 1.8×10-5C | B. | 8×10-6C | C. | 1.0×10-5C | D. | 2.6×10-5C |
| A. |  | B. | 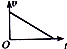 | C. | 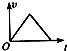 | D. |  |
| A. | 物体的重力势能一定大于零 | |
| B. | 在地面上的物体的重力势能一定等于零 | |
| C. | 物体的重力势能与零势能面的选取有关 | |
| D. | 物体重力势能的变化量与零势能面的选取有关 |
 如图所示,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直.在电磁场区域中,有一个固定在竖直平面内的光滑绝缘圆环,环上套有一个带正电的小球.O点为圆环的圆心,a、b、c为圆环上的三个点,a点为最高点,c点为最低点,bO沿水平方向.已知小球所受电场力与重力大小相等.现将小球从环的顶端a点由静止释放,下列判断正确的是( )
如图所示,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直.在电磁场区域中,有一个固定在竖直平面内的光滑绝缘圆环,环上套有一个带正电的小球.O点为圆环的圆心,a、b、c为圆环上的三个点,a点为最高点,c点为最低点,bO沿水平方向.已知小球所受电场力与重力大小相等.现将小球从环的顶端a点由静止释放,下列判断正确的是( )| A. | 当小球运动到b点时,小球受到的洛伦兹力最大 | |
| B. | 当小球运动到c点时,小球受到的支持力一定大于重力 | |
| C. | 小球从a点运动到b点,重力势能减小,电势能增大 | |
| D. | 小球从b点运动到c点,电势能增大,动能先增大后减小 |
 如图所示,A、B、C三个物体如图所示连接,整体处于静止状态,C与地面接触,B的上表面光滑,倾角为θ,已知mB=m,mC=mA=2m.
如图所示,A、B、C三个物体如图所示连接,整体处于静止状态,C与地面接触,B的上表面光滑,倾角为θ,已知mB=m,mC=mA=2m. 如图所示,重为0.2N的导体棒ab水平放置,与竖直放置的光滑金属导轨接触良好,导轨宽L=0.2m,匀强磁场垂直于导轨平面.当导体棒中的电流I=2A时,导体棒处于静止状态.问:
如图所示,重为0.2N的导体棒ab水平放置,与竖直放置的光滑金属导轨接触良好,导轨宽L=0.2m,匀强磁场垂直于导轨平面.当导体棒中的电流I=2A时,导体棒处于静止状态.问: