题目内容
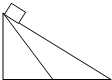 两个质量相等的物体,分别从两个高度相等而倾角不同的光滑斜面顶从静止开始下滑,则下列说法正确的是( )
两个质量相等的物体,分别从两个高度相等而倾角不同的光滑斜面顶从静止开始下滑,则下列说法正确的是( )①到达底部时重力的功率相等
②到达底部时速度相等
③下滑过程中重力做的功相等
④到达底部时动能相等.
分析:重力的功可由高度判断,功率可根据pG=mgvcosθ来判断;
小球到达最低点时速率,动能可通过动能定理来判断;
小球到达最低点时速率,动能可通过动能定理来判断;
解答:解:①②:小球从静止到最低点的过程运用动能定理
mv2-0=mgh,所以两种情况下的末速度大小相等,而θ不等,根据pG=mgvcosθ可知三个小球到达底端时重力的功率不相同.故①错误,动能相等则速率相等,但是方向不同,故②错误.
③:重力做功只与初末位置高度差有关,故重力的功为mgh,到底端重力的功相等,故③正确.
④:由动能定理mgh=
mv2,重力做功相等,故动能相等,故④正确,故D正确
故选:D.
| 1 |
| 2 |
③:重力做功只与初末位置高度差有关,故重力的功为mgh,到底端重力的功相等,故③正确.
④:由动能定理mgh=
| 1 |
| 2 |
故选:D.
点评:本题考查了动能定理得应用,重点掌握重力势能的变化和重力做功的关系,难度不大,属于基础题.

练习册系列答案
相关题目
两个质量相等的物体,分别从两个高度相等而倾角不同的光滑斜面顶端从静止开始下滑到达底部,则下列说法正确的是( )
| A、到达底部时重力的瞬时功率相等 | B、下滑过程中重力的平均功率相等 | C、到达底部时速度大小相等 | D、下滑过程中重力做功相等 |
 如图所示,在光滑的水平地面上,有两个质量相等的物体,中间用劲度系数为k的轻质弹簧相连,在外力作用下运动,已知F1>F2,当运动达到稳定时,弹簧的伸长量为
如图所示,在光滑的水平地面上,有两个质量相等的物体,中间用劲度系数为k的轻质弹簧相连,在外力作用下运动,已知F1>F2,当运动达到稳定时,弹簧的伸长量为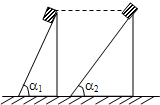 如图所示,两个质量相等的物体在同一高度沿倾角不同的两个斜面由静止加速下滑,α1>α2,且第一个斜面光滑,第二个斜面粗糙,从顶端滑到底端的过程中,重力对物体做功分别为W1和W2,则( )
如图所示,两个质量相等的物体在同一高度沿倾角不同的两个斜面由静止加速下滑,α1>α2,且第一个斜面光滑,第二个斜面粗糙,从顶端滑到底端的过程中,重力对物体做功分别为W1和W2,则( )