题目内容

（2011?江苏一模）如图所示，粗糙斜面AB与竖直平面内的光滑圆弧轨道BCD相切于B点，圆弧轨道的半径为R，C点在圆心O的正下方，D点与圆心O在同一水平线上，∠COB=θ．现有质量为m的物块从D点无初速释放，物块与斜面间的动摩擦因数为μ，重力加速度为g．求：
（1）物块第一次通过C点时对轨道压力的大小；
（2）物块在斜面上运动离B点的最远距离．
分析：物块从D到C，根据机械能守恒定律得C点速度．
物块经C点，根据牛顿第二定律求得通过C点时对轨道压力的大小．
小物体通过圆弧轨道后，由动能定理求得物块在斜面上运动离B点的最远距离．
解答：解：（1）物块从D到C，根据机械能守恒定律，得
mgR=
1
2
mv2
物块经C点，根据牛顿第二定律，得
FN-mg=m
v2
R

由以上两式得支持力大小FN=3mg  
由牛顿第三定律得，物块对轨道的压力大小为3mg．
（2）小物体通过圆弧轨道后，在斜面上运动到最大距离S时速度为0，
由动能定理可得mgRcosθ-mgSsinθ-μmgScosθ=0
故 S=
Rcosθ
sinθ+μcosθ

答：（1）物块第一次通过C点时对轨道压力的大小是3mg；
（2）物块在斜面上运动离B点的最远距离是
Rcosθ
sinθ+μcosθ
．
点评：本题考查了圆周运动中牛顿第二定律相关公式的应用，在不涉及到具体的运动过程或求变力做功时，运用动能定理解题比较简洁、方便．
练习册系列答案
相关题目
（2011?江苏一模）如图甲所示，理想变压器原、副线圈的匝数比为10：1，电阻R=22Ω，各电表均为理想电表．原线圈输入电压的变化规律如图乙所示．下列说法正确的是（　　）
 
（2011?江苏一模）如图所示，条形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场，磁感应强度B的大小均为0.3T，AA′、BB′、CC′、DD′为磁场边界，它们相互平行，条形区域的长度足够长，磁场宽度及BB′、CC′之间的距离d=1m．一束带正电的某种粒子从AA′上的O点以沿与AA′成60°角、大小不同的速度射入磁场，当粒子的速度小于某一值v0时，粒子在区域Ⅰ内的运动时间t0=4×10-6s；当粒子速度为v1时，刚好垂直边界BB′射出区域Ⅰ．取π≈3，不计粒子所受重力． 求：
（1）粒子的比荷
qm
；
（2）速度v0 和v1的大小；
（3）速度为v1的粒子从O到DD′所用的时间．
（2011?江苏一模）发光二极管在生产和生活中得到了广泛应用．图甲是一种发光二极管的实物图，正常使用时，带“+”号的一端接高电势，带“-”号的一端接低电势．某同学想描绘它的伏安特性曲线，实验测得它两端电压U和通过它电流I的数据如下表所示：
U/V 0 0.40 0.80 1.20 1.60 2.00 2.40 2.80
I/mA 0 0.9 2.3 4.3 6.8 12.0 19.0 30.0
（1）实验室提供的器材如下：
A．电压表（量程0-3V，内阻约10kΩ）     B．电压表（量程0-15V，内阻约25kΩ）
C．电流表（量程0-50mA，内阻约50Ω）   D．电流表（量程0-0.6A，内阻约1Ω）
E．滑动变阻器（阻值范围0-10Ω，允许最大电流3A）
F．电源（电动势6V，内阻不计）   G．开关，导线
该同学做实验时，电压表选用的是
A
A
，电流表选用的是
C
C
（填选项字母）．
 （2）请在图乙中以笔划线代替导线，按实验要求将实物图中的连线补充完整．
（3）根据表中数据，在图丙所示的坐标纸中画出该发光二极管的I-U图线．
（4）若此发光二极管的最佳工作电流为10mA，现将此发光二极管与电动势为3V、内阻不计的电池组相连，还需串联一个阻值R=
110
110
Ω的电阻，才能使它工作在最佳状态 （结果保留三位有效数字）．
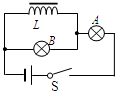（2011?江苏一模）如图，L是直流电阻为零、自感系数很大的线圈，A和B是两个相同的小灯泡，某时刻闭合开关S，通过A、B两灯泡中的电流IA、IB随时间t变化的图象，正确的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网