题目内容
1.小球A以速度v0向右运动,与静止的小球B发生碰撞,碰后A、B球的速度大小分别为$\frac{v_0}{4}、\frac{v_0}{2}$,则A、B两球的质量比可能是( )| A. | 1:2 | B. | 2:3 | C. | 3:2 | D. | 2:5 |
分析 两球碰撞过程系统所受合外力为零,系统动量守恒,应用动量守恒定律可以求出两球的质量之比.
解答 解:碰撞过程两球组成的系统动量守恒,取碰撞前A的速度方向为正方向.
若碰后A的速度方向与原来的方向相同时,碰后A的速度为$\frac{1}{4}$v0,
根据动量守恒定律得:mAv0=mA×$\frac{{v}_{0}}{4}$+mB×$\frac{{v}_{0}}{2}$,解得,mA:mB=2:3.
若碰后A的速度方向与原来的方向相反时,碰后A的速度为-$\frac{1}{4}$v0,
根据动量守恒定律得:mAv0=-mA×(-$\frac{1}{4}$v0)+mB×$\frac{{v}_{0}}{2}$,解得,mA:mB=2:5.
故选:BD.
点评 本题考查了求两球的质量之比,考查了动量守恒定律的应用,分析清楚球的运动过程是解题的关键,应用动量守恒定律可以解题;解题时考虑问题要全面,要讨论,否则会漏解.

练习册系列答案
相关题目
12.如图所示为甲、乙两物体沿同一直线运动的s-t图象,下列说法中正确的是( )


| A. | 两物体的初速度都为零 | |
| B. | 甲、乙两物体相遇时,速度大小相等 | |
| C. | 甲物体做变加速直线运动,乙物体做匀加速直线运动 | |
| D. | 在t1时间内两物体的平均速度大小相等 |
16.物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程.在对以下几位物理学家所做科学贡献的叙述中,正确的说法是( )
| A. | 英国物理学家卡文迪许用实验的方法测出引力常量G | |
| B. | 牛顿通过开普勒行星运动定律和牛顿运动定律发现了万有引力定律 | |
| C. | 牛顿通过苹果落地发现了万有引力定律 | |
| D. | 开普勒经过多年的天文观测和记录,提出了“日心说”的观点 |
6. 如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )
如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )
 如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )
如图所示,质量为m的物体用细线悬挂保持静止,其中OB是水平的.保持结点O的位置不动,手持OA绳的A端,使其缓慢向上转动至竖直位置,在此过程中,OA绳上的拉力大小( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 最大值是mg | D. | 最小值是mg |
13. 如图,一带绝缘座的中性导体置于一带负电荷的小球附近,此时导体的电势为φ1,然后用手触摸导体的左端(即将导体的左端接地),此时导体的电势为φ2,把触摸导体的手松开后,再将小球移开,此时导体的电势为φ3,取大地或无穷远处的电势为零,则φ1、φ2、φ3的高低关系为( )
如图,一带绝缘座的中性导体置于一带负电荷的小球附近,此时导体的电势为φ1,然后用手触摸导体的左端(即将导体的左端接地),此时导体的电势为φ2,把触摸导体的手松开后,再将小球移开,此时导体的电势为φ3,取大地或无穷远处的电势为零,则φ1、φ2、φ3的高低关系为( )
 如图,一带绝缘座的中性导体置于一带负电荷的小球附近,此时导体的电势为φ1,然后用手触摸导体的左端(即将导体的左端接地),此时导体的电势为φ2,把触摸导体的手松开后,再将小球移开,此时导体的电势为φ3,取大地或无穷远处的电势为零,则φ1、φ2、φ3的高低关系为( )
如图,一带绝缘座的中性导体置于一带负电荷的小球附近,此时导体的电势为φ1,然后用手触摸导体的左端(即将导体的左端接地),此时导体的电势为φ2,把触摸导体的手松开后,再将小球移开,此时导体的电势为φ3,取大地或无穷远处的电势为零,则φ1、φ2、φ3的高低关系为( )| A. | φ1>φ2>φ3 | B. | φ1<φ2<φ3 | C. | φ1=φ2=φ3 | D. | φ1>φ2=φ3 |
10.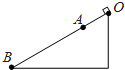 如图所示,水平地面上固定着总长为L的斜面,一小物块(可视为质点)从斜面顶端O点由静止开始下滑,到达斜面底端的B点时速度大小为v,所用时间为t;若小物块到达斜面上某一点A时速度大小为$\frac{1}{2}$v,OA距离为LA,由O到A的时间为tA.下列说法正确的是( )
如图所示,水平地面上固定着总长为L的斜面,一小物块(可视为质点)从斜面顶端O点由静止开始下滑,到达斜面底端的B点时速度大小为v,所用时间为t;若小物块到达斜面上某一点A时速度大小为$\frac{1}{2}$v,OA距离为LA,由O到A的时间为tA.下列说法正确的是( )
 如图所示,水平地面上固定着总长为L的斜面,一小物块(可视为质点)从斜面顶端O点由静止开始下滑,到达斜面底端的B点时速度大小为v,所用时间为t;若小物块到达斜面上某一点A时速度大小为$\frac{1}{2}$v,OA距离为LA,由O到A的时间为tA.下列说法正确的是( )
如图所示,水平地面上固定着总长为L的斜面,一小物块(可视为质点)从斜面顶端O点由静止开始下滑,到达斜面底端的B点时速度大小为v,所用时间为t;若小物块到达斜面上某一点A时速度大小为$\frac{1}{2}$v,OA距离为LA,由O到A的时间为tA.下列说法正确的是( )| A. | LA=$\frac{L}{2}$ | B. | LA=$\frac{L}{4}$ | C. | tA=$\frac{t}{2}$ | D. | tA=$\frac{t}{\sqrt{2}}$ |
11. 如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )
如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )
 如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )
如图所示直线是电场中的一条电场线,A、B是该线上的两点.一负电荷由A点以一定初速度沿电场线从A运动到B,运动过程中的速度-时间图线如图乙所示,则下列说法中正确的是( )| A. | 该电场是匀强电场 | |
| B. | A、B两点的电势相比一定是φA<φB | |
| C. | A、B两点的场强大小相比一定是EA<EB | |
| D. | 该电荷在两点的电势能大小相比一定是EpA<EpB |
 如图所示,在倾角为α的光滑斜面上,垂直纸面放置一根长为L、质量为m的直导体棒,导体棒中通有大小为I、方向垂直纸面向里的电流,欲使导体棒静止在斜面上,可以施加方向垂直于导体棒的匀强磁场.求:
如图所示,在倾角为α的光滑斜面上,垂直纸面放置一根长为L、质量为m的直导体棒,导体棒中通有大小为I、方向垂直纸面向里的电流,欲使导体棒静止在斜面上,可以施加方向垂直于导体棒的匀强磁场.求: 如图所示,一根长为L的铝棒用两个倔强系数为k的弹簧水平地悬吊在匀强磁场中,磁场方向垂直于纸面向里.当棒中通以向右的电流I,系统重新平衡后,两弹簧的伸长量与未通电时相比均改变了△x;若通以向左的电流I时,系统重新平衡后,两弹簧的伸长量与未通电时相比均改变了△y.求磁感应强度B.
如图所示,一根长为L的铝棒用两个倔强系数为k的弹簧水平地悬吊在匀强磁场中,磁场方向垂直于纸面向里.当棒中通以向右的电流I,系统重新平衡后,两弹簧的伸长量与未通电时相比均改变了△x;若通以向左的电流I时,系统重新平衡后,两弹簧的伸长量与未通电时相比均改变了△y.求磁感应强度B.