题目内容
11.如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1kg的木板与轻弹簧接触但不拴接,弹簧与斜面平行,且为原长,在木板右端放一质量为m=2kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3m/s、方向平行斜面向下的速度,经过时间t=0.75s,金属块与木板相对静止,此时弹簧被压缩x=0.5m(弹簧处于弹性限度内)已知sin θ=0.28、cos θ=0.96,g取10m/s2
(1)求木板开始运动瞬间的加速度大小;
(2)求金属块与木板相对静止时弹簧的弹性势能.
分析 (1)运用隔离法分别对金属块和长木板进行受力分析,根据牛顿第二定律求加速度;
(2)根据动能定理求得弹簧压缩过程中做的功,再根据弹力做功与弹性势能变化的关系求得弹簧的弹性势能;
解答 解(1)对金属块,由牛顿第二定律可知加速度大小为
a=μ1gcosθ-gsinθ=0.75×10×0.96-10×0.28m/s2=4.4m/s2,沿斜面向上
木板受到金属块的滑动摩擦力F1=μ1mgcosθ=0.75×2×10×0.96N=14.4N,沿斜面向下
木板受到斜面的滑动摩擦力
F2=μ2(M+m)gcosθ=0.25×(1+2)×10×0.96N=7.2N,沿斜面向上
木板开始运动瞬间的加速度a0=$\frac{Mgsinθ+F1-F2}{M}$=$\frac{1×10×0.28+14.4-7.2}{1}m/{s}^{2}$=10m/s2,沿斜面向下
(2)设金属块和木板达到共同速度为v2,对金属块,应用速度公式有
v2=v1-at=5.3-4.4×0.75m/s=2.0m/s
在此过程中分析木板,设弹簧对木板做功为W,其余力做功为Wx,
对木板运用动能定理得:Wx+W=$\frac{1}{2}$Mv${\;}_{2}^{2}$
又由受力分析得Wx=[μ1mgcosθ+Mgsinθ-μ2(M+m)gcosθ]x
[μ1mgcosθ+Mgsinθ-μ2(M+m)gcosθ]x+W=$\frac{1}{2}$M${v}_{2}^{2}$
代入相关数据解得:解得W=-3.0J,说明此时弹簧的弹性势能Ep=3.0J
答:(1)木板开始运动瞬间的加速度为10m/s2方向沿斜面向下;
(2)弹簧被压缩到P点时的弹性势能是3.0J;
点评 在应用牛顿运动定律和运动学公式解决问题时,要注意运动过程的分析,此类问题,还要对整个运动进行分段处理.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| A. | 陨石对地球的吸引的引力远小于地球对陨石的吸引力,所以陨石落向地球 | |
| B. | 陨石对地球的引力和地球对陨石的引力大小相等,但陨石质量小,加速度大,所以改变运动方向落向地球 | |
| C. | 太阳对陨石的引力小于地球的引力,所以陨石落向地球 | |
| D. | 陨石是因受到其他的排斥力落向地球 |
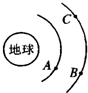
| A. | 线速度大小关系:vA<vB=vC | B. | 加速度大小关系:aA>aB=aC | ||
| C. | 向心力大小关系:FA=FB<FC | D. | 周期关系:TA<TB=TC |
 质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示,开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示,开始时OA边处于水平位置,由静止释放,则( )| A. | A球的最大速度为$\frac{2}{3}$$\sqrt{6(\sqrt{2}-1)gl}$ | |
| B. | A球的速度最大时,其重力势能最小 | |
| C. | A球的速度最大时,两直角边与竖直方向的夹角为45° | |
| D. | B球上升的最大高度为l |
| A. | 位移的大小可能小于4m | B. | 位移的大小可能大于4m | ||
| C. | 加速度的大小可能小于4m/s2 | D. | 加速度的大小可能大于10m/s2 |
 汽车由甲地开出,沿平直公路开到乙地时,刚好停止运动.它的速度图象如图所示.在0~t0和t0~3t0两段时间内,汽车的( )
汽车由甲地开出,沿平直公路开到乙地时,刚好停止运动.它的速度图象如图所示.在0~t0和t0~3t0两段时间内,汽车的( )| A. | 加速度大小之比为2:1 | B. | 位移大小之比为1:2 | ||
| C. | 牵引力与摩擦力大小之为2:1 | D. | 平速度大小之比为1:1 |
| A. | 可能变大 | B. | 可能变小 | C. | 一定不变 | D. | 不能确定 |