题目内容
如图所示，L1和L2为距离d=0.1m的两平行的虚线，L1上方和L2下方都是垂直纸面向里的磁感应强度为B=0.20T的匀强磁场，A、B两点都在L2上，质量为m=1.67×10-27kg、电量Q=1.60×10-19C的质子，从A点以v0=5.0×105m/s的速度与L2成θ=45°角斜向上射出，经过上方和下方的磁场偏转后正好经过B点，经过B点时速度方向也斜向上，求（结果保留两位有效数字）（1）质子在磁场中做圆周运动的半径；
（2）A、B两点间的最短距离；
（3）质子由A点运动到B点的时间的可能值．
分析：（1）根据洛伦兹力力提供向心力列方程求解半径；
（2）作出粒子的运动轨迹图，通过几何关系求出A、B两点间的最短距离．
（3）作出粒子运动轨迹，根据几何关系可知，粒子在磁场中的轨道半径正好等于弦长，从而求出能够回到B点的几何关系．
（2）作出粒子的运动轨迹图，通过几何关系求出A、B两点间的最短距离．
（3）作出粒子运动轨迹，根据几何关系可知，粒子在磁场中的轨道半径正好等于弦长，从而求出能够回到B点的几何关系．
解答：解：（1）质子在磁场中做匀速圆周运动，洛仑兹力提供向心力，设半径为R，有：
qv0B=
①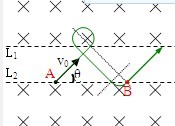
R=
=2.6×10-2m②
（2）质子由A点运动到B点可重复若干周期，其中一个周期内的运动情况如图所示，由几何关系知，A、B两点间的最短距离为：
dmin=
=2d=0.2m③
（3）质子在磁场中运动的时间为一个圆周运动的周期T（优弧加劣弧恰好为一个整圆），在L1、L2中运动的时间为t，则有：
T=
，t=
④
所以：tAB=T+t=
+
=8.9×10-7s ⑤
答：（1）质子在磁场中做圆周运动的半径为2.6×10-2m；
（2）A、B两点间的最短距离dmin为0.2m；
（3）质子由A点运动到B点的时间的可能值8.9×10-7s．
qv0B=
| mv02 |
| R |
R=
| mv0 |
| qB |
（2）质子由A点运动到B点可重复若干周期，其中一个周期内的运动情况如图所示，由几何关系知，A、B两点间的最短距离为：
dmin=
| 2d |
| tanθ |
（3）质子在磁场中运动的时间为一个圆周运动的周期T（优弧加劣弧恰好为一个整圆），在L1、L2中运动的时间为t，则有：
T=
| 2πm |
| qB |
| 2d |
| v0sinθ |
所以：tAB=T+t=
| 2πm |
| qB |
| 2d |
| v0sinθ |
答：（1）质子在磁场中做圆周运动的半径为2.6×10-2m；
（2）A、B两点间的最短距离dmin为0.2m；
（3）质子由A点运动到B点的时间的可能值8.9×10-7s．
点评：能根据粒子的受力情况判断粒子的运动情况，根据粒子运动轨迹和几何关系求解是关键．
练习册系列答案
快乐5加2金卷系列答案
相关题目
（2010?沈阳二模）如图所示，L1和L2为两条平行的虚线，L1上方和L2下方都是垂直纸面向外的磁感应强度相同的匀强磁场，A、B两点都在L1上．带电粒子从A点以初速V斜向下与L1成45°角射出，经过偏转后正好过B点，经过B点时速度方向也斜向下，且方向与A点方向相同．不计重力影响，下列说法中正确的是（ ）
如图所示，L1和L2是高压输电线，利用甲、乙可以测输电线路电压和电流．若已知甲的原副线圈匝数比为1000：1，乙的原副线圈匝数比为1：l00，并且已知加在电压表两端的电压为220V，通过电流表的电流为10A，则（ ）
如图所示，L1和L2为平行的虚线，L1上方和L2 下方都是垂直纸面向里的磁感应强度相同的匀强磁场，AB两点都在L2上，带电粒子从A点以初速v与L2成30°斜向上射出，经过偏转后正好过B点，经过B点时速度方向也斜向上，不计粒子重力．下列说法中正确的是（ ）
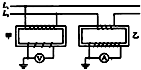如图所示，L1和L2是输电线，甲是电压互感器，乙是电流互感器．若已知变压比为1000：1，变流比为100：1，并且知道电压表示数为220V，电流表示数为10A，则输电线的输送功率为（ ）| A、2.2×10-2W | B、2.2×103 W | C、2.2×104W | D、2.2×108 W |