题目内容
4.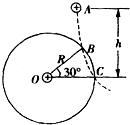 如图所示,在O点处放置一个正电荷.在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆 (图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法不正确的是( )
如图所示,在O点处放置一个正电荷.在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆 (图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法不正确的是( )| A. | 小球通过C点的速度大小是$\sqrt{2gh}$ | |
| B. | 小球在B、C两点的电势能不等 | |
| C. | 小球由A点到C点的过程中电势能一直都在减少 | |
| D. | 小球由A点到C点机械能的损失是mg(h-$\frac{R}{2}$)-$\frac{1}{2}$mv2 |
分析 小球下落过程中,受到重力和电场力,由于B、C两点处于同一等势面上,故从B到C过程电场力做功为零;根据电场力做功判断电势能的变化情况;根据总功判断动能变化情况.
解答 解:A、小球从A点到C点的过程中,电场力总体上做的是负功,重力做正功,由动能定理可以知道电荷在C点的大小是$\sqrt{{v}^{2}+gR}$,因此C点的速度小于$\sqrt{2gh}$,故A错误;B、到O点相等的B、C两点位于同一个等势面上,所以小球在B、C两点的电势能相等.故B错误;
C、小球由B点到C点的过程中电势能先增大后减小,所以小球由A点到C点的过程中电势能先增大后减小.故C错误;
D、小球由A点到C点机械能的损失就是除了重力以外的其他力做的功,即电场力做的功.
由动能定理得
mgh+W电=$\frac{1}{2}m{v}_{c}^{2}$ 则:
W电=$\frac{1}{2}m{v}_{c}^{2}-mgh$=$\frac{1}{2}$mv2+mg$\frac{R}{2}$-mgh
即电势能增加了mg(h-$\frac{R}{2}$)-$\frac{1}{2}$mv2,机械能减少了mg(h-$\frac{R}{2}$)-$\frac{1}{2}$mv2
故D正确;
本题选择不正确的,故选:ABC
点评 本题关键是明确几种功能关系的具体形式:
总功是动能变化的量度;
电场力做功是电势能变化的量度;
除重力外其余力做的功是机械能变化的量度.

练习册系列答案
相关题目
14. 用绝缘线L1将A、B连起来,再用绝缘细线L2将A悬于O点,然后将整个装置置于水平方向的匀强电场中,静止时L1向左偏离竖直方向,L2恰好处于竖直方向,如图所示,据此作出的判断正确的是( )
用绝缘线L1将A、B连起来,再用绝缘细线L2将A悬于O点,然后将整个装置置于水平方向的匀强电场中,静止时L1向左偏离竖直方向,L2恰好处于竖直方向,如图所示,据此作出的判断正确的是( )
 用绝缘线L1将A、B连起来,再用绝缘细线L2将A悬于O点,然后将整个装置置于水平方向的匀强电场中,静止时L1向左偏离竖直方向,L2恰好处于竖直方向,如图所示,据此作出的判断正确的是( )
用绝缘线L1将A、B连起来,再用绝缘细线L2将A悬于O点,然后将整个装置置于水平方向的匀强电场中,静止时L1向左偏离竖直方向,L2恰好处于竖直方向,如图所示,据此作出的判断正确的是( )| A. | 只能断定m1=m2 | B. | 只能断定q1=q2 | ||
| C. | 能断定m1=m2且q1=q2 | D. | 可以断定m1=m2且q1<q2 |
13.假设地球和火星都绕太阳做匀速圆周运动,已知地球到太阳的距离小于火星到太阳的距离,那么( )
| A. | 地球公转的线速度小于火星公转的线速度 | |
| B. | 地球公转的周期大于火星的公转周期 | |
| C. | 地球公转的角速度大于火星公转的角速度 | |
| D. | 地球公转的加速度小于火星公转的加速度 |
14.以下有关力的说法正确的有( )
| A. | 受静摩擦力作用的物体一定相对地面静止 | |
| B. | 滑动摩擦力也可以作用在相对地面静止的物体上 | |
| C. | 用一细竹竿拨动水中的木头,木头受到竹竿的推力是由于竹竿发生形变而产生的 | |
| D. | 三个大小分别为3N、5N、20N的共点力合力范围是0~28N |

 欲用伏安法测定一段阻值约为5Ω左右的金属导线的电阻,要求测量结果尽量准确,现备有以下器材:
欲用伏安法测定一段阻值约为5Ω左右的金属导线的电阻,要求测量结果尽量准确,现备有以下器材: