Question

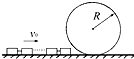如图所示，娱乐场空中列车由许多节完全相同的车厢组成，列车先沿水平轨道行驶，然后滑上半径为R的空中圆环形光滑轨道．若列车全长为L（L＞2πR），R远大于一节车厢的长度和高度，那么列车在运行到圆环前的速度v₀至少多大，才能使整个列车安全通过圆环轨道？

Answer 1

分析：先根据向心力公式求出车厢恰能滑到最高处时的临界速度，对布满在轨道上车厢整体运用动能定理列式即可求解．

解答：解：滑上轨道前列车速度的最小值v₀与轨道最高处车厢应具有的速度的最小值v相对应．这里v代表车厢恰能滑到最高处，且对轨道无弹力的临界状态．由：
mg=

mv2

R

得：v=

gR

另外列车势能还增加了M′gh，其中M′为布满在轨道上车厢的质量，
M′=M

2πR

L

h为它们的平均高度，h=R
由以上分析可得：

1

2

Mv₀²=

1

2

Mv²+M

2πR

L

gR
解得：v0=

Rg+4πR2 L

答：列车在运行到圆环前的速度v₀至少为

Rg+4πR2 L

，才能使整个列车安全通过圆环轨道．

点评：本题主要考查了向心力公式及动能定理的直接应用，难度适中．