题目内容
13. 如图所示,两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上,导轨上端连接一个定值电阻.导体棒a和b放在导轨上,与导轨垂直并良好接触.斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场.现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止.当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨.当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动.已知a棒、b棒和定值电阻的阻值均为R,b棒的质量为m,重力加速度为g,导轨电阻不计.求:
如图所示,两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上,导轨上端连接一个定值电阻.导体棒a和b放在导轨上,与导轨垂直并良好接触.斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场.现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止.当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨.当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动.已知a棒、b棒和定值电阻的阻值均为R,b棒的质量为m,重力加速度为g,导轨电阻不计.求:(1)a棒在磁场中沿导轨向上运动的过程中,a棒中的电流强度Ia与定值电阻R中的电流强度IR之比;
(2)a棒质量ma;
(3)a棒在磁场中沿导轨向上运动时所受的拉力F.
分析 (1)a棒相当于电源,b棒与R并联,由串并联电路的电流规律可得出两电阻中电流之比;
(2)对b棒由受力平衡可求得Ib,由(1)可求得Ia;因a棒离开磁场后机械能守恒,故返回磁场时的速度相等,则由返回磁场时做匀速运动可由受力平衡得出a的速度,联立各式可得出a的质量;
(3)已知Ib,则由安培力公式可求得b受到的安培力F,再由平衡条件求拉力F.
解答 解:(1)a棒沿导轨向上运动时,a棒、b棒及电阻R中的电流强度分别为Ia、Ib、IR,有
IRR=IbR ①
Ia=IR+Ib ②
由①②解得 $\frac{{I}_{a}}{{I}_{R}}$=$\frac{2}{1}$ ③
(2)由于a棒在PQ上方滑动过程中机械能守恒,因而a棒在磁场中向上滑动的速度大小v1
与在磁场中向下滑动的速度大小v2相等,即 v1=v2=v ④
设磁场的磁感应强度为B,导体棒长为L.
a棒在磁场中运动时产生的感应电动势为E=BLv ⑤
当a棒沿斜面向上运动时 Ib=$\frac{E}{2×\frac{3R}{2}}$ ⑥
b棒静止,有 BIbL=mgsin θ ⑦
向下匀速运动时,a棒中的电流为Ia′,则
Ia′=$\frac{E}{2R}$ ⑧
BIa′L=magsin θ ⑨
由④⑤⑥⑦⑧⑨解得 ma=$\frac{3}{2}$m
(3)由题知导体棒a沿斜面向上运动时,所受拉力
F=BIaL+magsin θ
联立以上各式解得F=$\frac{7}{2}$mgsin θ
答:
(1)a棒在磁场中沿导轨向上运动的过程中,a棒中的电流强度Ia与定值电阻R中的电流强度IR之比是2:1;
(2)a棒质量ma是$\frac{3}{2}$m.
(3)a棒在磁场中沿导轨向上运动时所受的拉力F是$\frac{7}{2}$mgsinθ.
点评 电磁感应常常与能量及受力结合,在分析此类问题时要注意物体的运动状态,从而灵活地选择物理规律求解.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案 如图a、b、c是地球大气层外圆轨道运动的三颗人造卫星,a、b质量相同而小于c质量,下列判断正确的是( )
如图a、b、c是地球大气层外圆轨道运动的三颗人造卫星,a、b质量相同而小于c质量,下列判断正确的是( )①b、c线速度大小相等且小于a线速度
②b、c周期相等且大于a周期
③b、c向心加速度相等且大于a的向心加速度
④b受的引力最小.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
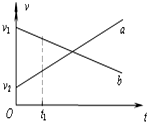 甲和乙两个物体在同一直线上运动,它们的速度-时间图象分别如图中的a和b所示.在t1时刻( )
甲和乙两个物体在同一直线上运动,它们的速度-时间图象分别如图中的a和b所示.在t1时刻( )| A. | 它们的运动方向相同 | B. | 它们的运动方向相反 | ||
| C. | a的速度比b的速度大 | D. | a、b的加速度方向相同 |
| A. | 电源电动势等于电源没有接入电路时两极间的电压 | |
| B. | 不同电源的电动势是一样的 | |
| C. | 电源电动势由电源本身的性质决定 | |
| D. | 电动势和电压的单位相同且均是标量 |
| A. | 一定大小相等 | B. | 方向有可能相同 | ||
| C. | 一定作用在同一个物体上 | D. | 两个力的性质一定相同 |
 在“探究求合力的方法”的实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套(如图).实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条,使橡皮条伸长,结点到达某一位置O.
在“探究求合力的方法”的实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套(如图).实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条,使橡皮条伸长,结点到达某一位置O.
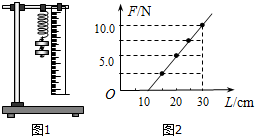 做“探索弹力与弹簧伸长量关系”的实验步骤如下:
做“探索弹力与弹簧伸长量关系”的实验步骤如下: