题目内容
(10分)为研究“在外力一定的条件下,物体的加速度与其质量间的关系”, 某同学设计了如图所示的实验装置,图中打点计时器的交流电源频率为f=50Hz。

⑴完成下列实验步骤中的填空:
①平衡小车所受的阻力:小吊盘中不放物块,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列 的点;
②按住小车,在小吊盘中放入适当质量的物块,在小车中放入砝码;
③打开打点计时器电源,释放小车,获得带有点迹的纸带,在纸带上标出小车中砝码的质量m;
④按住小车,改变小车中砝码的质量,重复步骤③;
⑤在每条纸带上清晰的部分,每5个间隔标注一个计数点,测量相邻计数点的间距s1,s2,…,求出与不同m相对应的加速度a;
⑥以砝码的质量m为横坐标, 为纵坐标,在坐标纸上作出
为纵坐标,在坐标纸上作出 -m关系图线。
-m关系图线。
⑵完成下列填空:
①本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是 ;
②下图为用米尺测量某一纸带的情况,a可用s1、s3和f表示为a= ,由图可读出s1、s2、s3,其中s1= cm,代入各数据,便可求得加速度的大小;

③下图为所得实验图线的示意图,设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为 ,小车的质量为 。


⑴完成下列实验步骤中的填空:
①平衡小车所受的阻力:小吊盘中不放物块,调整木板右端的高度,用手轻拨小车,直到打点计时器打出一系列 的点;
②按住小车,在小吊盘中放入适当质量的物块,在小车中放入砝码;
③打开打点计时器电源,释放小车,获得带有点迹的纸带,在纸带上标出小车中砝码的质量m;
④按住小车,改变小车中砝码的质量,重复步骤③;
⑤在每条纸带上清晰的部分,每5个间隔标注一个计数点,测量相邻计数点的间距s1,s2,…,求出与不同m相对应的加速度a;
⑥以砝码的质量m为横坐标,
 为纵坐标,在坐标纸上作出
为纵坐标,在坐标纸上作出 -m关系图线。
-m关系图线。⑵完成下列填空:
①本实验中,为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是 ;
②下图为用米尺测量某一纸带的情况,a可用s1、s3和f表示为a= ,由图可读出s1、s2、s3,其中s1= cm,代入各数据,便可求得加速度的大小;

③下图为所得实验图线的示意图,设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为 ,小车的质量为 。

⑴间隔相等;⑵①远小于小车的质量;② ,2.42(2.39~2.45cm之间均正确);③
,2.42(2.39~2.45cm之间均正确);③ ,
, 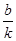 。
。
 ,2.42(2.39~2.45cm之间均正确);③
,2.42(2.39~2.45cm之间均正确);③ ,
, 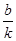 。
。试题分析:⑴①平衡摩擦力时,如果小车的重力沿板方向的分力正好等于摩擦力,给小车一个速度,小车将做匀速运动,因此打点计时器打出的点应该是间隔基本相等的;
⑵①由于细线不可伸长,因此小吊盘(包括物块)、小车、砝码一起运动的加速度大小相等,设小吊盘(包括物块)的质量为Δm,对小吊盘(包括物块)根据牛顿第二定律有:Δmg-F=Δma,解得:F=
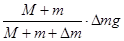 ,化简得:F=
,化简得:F= ,当Δm
,当Δm (M+m)时F≈Δmg,即F应与m无关,此时在改变小车中砝码的质量m时,小车所受的拉力近似不变,因此为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是:远小于小车和小车中砝码的质量之和,而砝码的质量m可以任意改变,可取到0,所以应满足的条件是:小吊盘和盘中物块的质量之和远小于小车的质量;
(M+m)时F≈Δmg,即F应与m无关,此时在改变小车中砝码的质量m时,小车所受的拉力近似不变,因此为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是:远小于小车和小车中砝码的质量之和,而砝码的质量m可以任意改变,可取到0,所以应满足的条件是:小吊盘和盘中物块的质量之和远小于小车的质量;②根据匀变速直线运动规律可知,相邻相等时间内的位移之差相等,即:Δs=aT 2,又由题意可知打点的时间间隔为Δt、每5个间隔标注一个计数点,因此相邻计数点之间的时间间隔为:T=5Δt,Δt=
 有:s3-s1=2aT 2,解得:a=
有:s3-s1=2aT 2,解得:a= ,根据题图可读出s1=36.7mm-12.5mm=2.42cm(由于刻度尺读数时要有估读位,因此读数在2.39~2.45cm之间均正确);
,根据题图可读出s1=36.7mm-12.5mm=2.42cm(由于刻度尺读数时要有估读位,因此读数在2.39~2.45cm之间均正确);③设细线对小车的拉力为F,小车的质量为M,砝码随小车一起加速运动的加速度为a,根据牛顿第二定律有:F=(M+m)a,解得:
 =
= +
+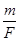 ,所以,k=
,所以,k=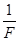 ,b=
,b= ,解得:F=
,解得:F= ,M=
,M=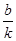 ,即小车受到的拉力为
,即小车受到的拉力为 ,小车的质量为
,小车的质量为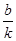 。
。
练习册系列答案
相关题目

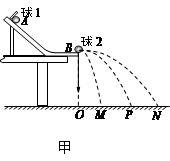
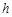
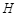
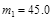 g,
g,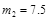 g,小球落地点的平均位置距
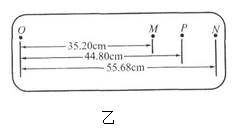
g,小球落地点的平均位置距 点的距离如图乙所示。有同学认为,在上述实验中仅更换两个小球的材质,其它条件不变,可以使被碰小球做平抛运动的射程增大。请你用已知的数据,分析和计算出被碰小球
点的距离如图乙所示。有同学认为,在上述实验中仅更换两个小球的材质,其它条件不变,可以使被碰小球做平抛运动的射程增大。请你用已知的数据,分析和计算出被碰小球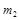 平抛运动射程
平抛运动射程 的最大值为
的最大值为  。
。

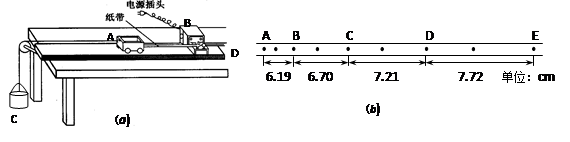





 、
、 、
、 ……
…… 草图
草图 ;如果不是直线,可考虑是否存在
;如果不是直线,可考虑是否存在 ,
, 等关系。
等关系。

