题目内容
20.已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T.万有引力常量为G,月球体积为V=$\frac{4}{3}$πR3,下列说法正确的是( )| A. | 飞船的线速度大小为$\frac{4πR}{T}$ | B. | 月球表面重力加速度为$\frac{32{π}^{2}}{{T}^{2}}$R | ||
| C. | 月球密度为$\frac{3π}{G{T}^{2}}$ | D. | 月球质量为$\frac{16{π}^{2}{R}^{3}}{G{T}^{2}}$ |
分析 飞船在距月球表面高度为R的圆轨道上飞行,做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律列式;在月球表面,重力等于万有引力,根据万有引力定律列式求解.
解答 解:A、已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T,
根据圆周运动公式得飞船的线速度大小为v=$\frac{4πR}{T}$,故A正确;
B、根据万有引力等于向心力得:$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,r=2R
在月球表面,根据万有引力等于重力$\frac{GMm}{{R}^{2}}$=mg,
解得月球表面重力加速度为g=$\frac{32{π}^{2}}{{T}^{2}}$R,月球质量M=$\frac{3{{2π}^{2}R}^{3}}{{GT}^{2}}$,故B正确,D错误;
C、月球密度ρ=$\frac{M}{\frac{4{πR}^{3}}{3}}$=$\frac{24π}{{GT}^{2}}$,故C错误;
故选:AB.
点评 本题是卫星类型的问题,常常建立这样的模型:环绕天体绕中心天体做匀速圆周运动,由中心天体的万有引力提供向心力.重力加速度g是联系星球表面宏观物体运动和天体运动的桥梁.

练习册系列答案
相关题目
11. 如图甲所示,在竖直方向分布均匀的磁场中水平放置一个金属圆环,圆环所围面积为0.1m2,圆环电阻为0.2Ω,在第1s内感应电流I沿顺时针方向(俯视),磁场的磁感应强度B随时间t的变化规律如图乙所示,其中4s~5s的时间段为直线,下列判断正确的是( )
如图甲所示,在竖直方向分布均匀的磁场中水平放置一个金属圆环,圆环所围面积为0.1m2,圆环电阻为0.2Ω,在第1s内感应电流I沿顺时针方向(俯视),磁场的磁感应强度B随时间t的变化规律如图乙所示,其中4s~5s的时间段为直线,下列判断正确的是( )
 如图甲所示,在竖直方向分布均匀的磁场中水平放置一个金属圆环,圆环所围面积为0.1m2,圆环电阻为0.2Ω,在第1s内感应电流I沿顺时针方向(俯视),磁场的磁感应强度B随时间t的变化规律如图乙所示,其中4s~5s的时间段为直线,下列判断正确的是( )
如图甲所示,在竖直方向分布均匀的磁场中水平放置一个金属圆环,圆环所围面积为0.1m2,圆环电阻为0.2Ω,在第1s内感应电流I沿顺时针方向(俯视),磁场的磁感应强度B随时间t的变化规律如图乙所示,其中4s~5s的时间段为直线,下列判断正确的是( )| A. | 在0~2s时间段,感应电流先增大再减少 | |
| B. | 在2s~4s时间段,感应电流I沿顺时针方向 | |
| C. | 在4s~5s时间段内,感应电流I沿顺时针方向 | |
| D. | 在0~5时间段,圆环的最大发热功率为5.0×10-4W |
8.一定质量的理想气体的压强、内能的变化与气体体积和温度的关系是( )
| A. | 如果保持其体积不变,温度升高,则气体的压强增大,内能增大 | |
| B. | 如果保持其体积不变,温度升高,则气体的压强增大,内能减少 | |
| C. | 如果保持其温度不变,体积增大,则气体的压强减小,内能增大 | |
| D. | 如果保持其温度不变,体积增大,则气体的压强减小,内能不变 |
15.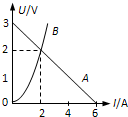 如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡的U-I图线,用该电源和小灯泡组成闭合电路时,电源的输出功率和电源的总功率分别是( )
如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡的U-I图线,用该电源和小灯泡组成闭合电路时,电源的输出功率和电源的总功率分别是( )
 如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡的U-I图线,用该电源和小灯泡组成闭合电路时,电源的输出功率和电源的总功率分别是( )
如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡的U-I图线,用该电源和小灯泡组成闭合电路时,电源的输出功率和电源的总功率分别是( )| A. | 4 W,8 W | B. | 4W,6 W | C. | 2 W,3 W | D. | 2 W,4 W |
12.北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,该系统由35颗卫星组成,卫星的轨道有三种:地球同步轨道、中轨道和倾斜轨道.其中,同步轨道半径大约是中轨道半径的1.5倍,那么同步卫星与中轨道卫星的周期比约为( )
| A. | $\sqrt{\frac{3}{2}}$ | B. | ($\frac{3}{2}$)${\;}^{\frac{2}{3}}$ | C. | ($\frac{3}{2}$)${\;}^{\frac{3}{2}}$ | D. | ($\frac{3}{2}$)2 |
10.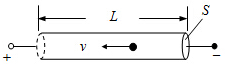 一根长为L、横截面积为S的金属棒,其材料的电阻率为ρ,棒内单位体积自由电子数为n,电子的质量为m,电荷量为e,在棒两端加上恒定的电压时,棒内产生电流,自由电子定向运动的平均速率为v,则金属棒内的电场强度大小为( )
一根长为L、横截面积为S的金属棒,其材料的电阻率为ρ,棒内单位体积自由电子数为n,电子的质量为m,电荷量为e,在棒两端加上恒定的电压时,棒内产生电流,自由电子定向运动的平均速率为v,则金属棒内的电场强度大小为( )
 一根长为L、横截面积为S的金属棒,其材料的电阻率为ρ,棒内单位体积自由电子数为n,电子的质量为m,电荷量为e,在棒两端加上恒定的电压时,棒内产生电流,自由电子定向运动的平均速率为v,则金属棒内的电场强度大小为( )
一根长为L、横截面积为S的金属棒,其材料的电阻率为ρ,棒内单位体积自由电子数为n,电子的质量为m,电荷量为e,在棒两端加上恒定的电压时,棒内产生电流,自由电子定向运动的平均速率为v,则金属棒内的电场强度大小为( )| A. | $\frac{m{v}^{2}}{2eL}$ | B. | $\frac{m{v}^{2}Sn}{e}$ | C. | ρnev | D. | $\frac{ρev}{SL}$ |
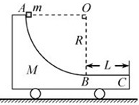 如图,质量为M的小车静止在光滑水平面上,小车AB段是半径为R的四分之一圆弧光滑轨道,BC段是长为L的水平粗糙轨道,两段轨道相切于B点.一质量为m的滑块在小车上从A点由静止开始沿轨道滑下,重力加速度为g.
如图,质量为M的小车静止在光滑水平面上,小车AB段是半径为R的四分之一圆弧光滑轨道,BC段是长为L的水平粗糙轨道,两段轨道相切于B点.一质量为m的滑块在小车上从A点由静止开始沿轨道滑下,重力加速度为g. 如图是过山车的部分模型图.模型图中光滑圆形轨道的半径R=8.1m,该光滑圆形轨道固定在倾角为α=37°斜轨道面上的Q点,圆形轨道的最高点A与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视作质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=$\frac{10}{81}$,不计空气阻力,过山车质量为20kg,取g=10m/s2,sin37°=0.6,cos37°=0.8.若小车恰好能通过圆形轨道的最高点A处,求:
如图是过山车的部分模型图.模型图中光滑圆形轨道的半径R=8.1m,该光滑圆形轨道固定在倾角为α=37°斜轨道面上的Q点,圆形轨道的最高点A与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视作质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=$\frac{10}{81}$,不计空气阻力,过山车质量为20kg,取g=10m/s2,sin37°=0.6,cos37°=0.8.若小车恰好能通过圆形轨道的最高点A处,求: 如图所示,两足够长平行光滑的金属导轨MN,PQ相距为L=1m,导轨平面与水平面夹角α=30°,导轨电阻不计,磁感应强度为B=1.0T的匀强磁场垂直导轨平面斜向下,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量m=0.01kg,电阻不计,定值电阻R1=30Ω,电阻箱电阻调到R2=120Ω,电容C=0.01F,g=10m/s2,现在将金属棒由静止释放.
如图所示,两足够长平行光滑的金属导轨MN,PQ相距为L=1m,导轨平面与水平面夹角α=30°,导轨电阻不计,磁感应强度为B=1.0T的匀强磁场垂直导轨平面斜向下,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量m=0.01kg,电阻不计,定值电阻R1=30Ω,电阻箱电阻调到R2=120Ω,电容C=0.01F,g=10m/s2,现在将金属棒由静止释放.