题目内容
某人离公共汽车尾部20m,以速度v向汽车匀速跑过去,与此同时,汽车以1m/s2的加速度从静止启动,作匀加速直线运动。试问:此人的速度v分别为下列数值时,能否追上汽车?如果能,要用多长时间?如果不能,则他与汽车之间的最小距离是多少?
(1)v=6m/s;
(2)v=7m/s。
(1)v=6m/s;
(2)v=7m/s。

解:设人出发点为初位置,则人与车的位移分别为
x人=vt
x车=x0+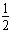 at2
at2
要追上汽车,则要求Δx=x车-x人=0
(1)当v=6m/s代入上式可得
Δx=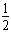 t2-6t+20=0
t2-6t+20=0
∵Δx=62-4×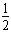 ×20<0
×20<0
∴Δx不能为零,不能追上
且Δx=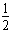 (t-6)2+2
(t-6)2+2
当t=6s时,Δx最小为2m
(2)当v=7m/s代入上式
Δx=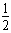 t2-7t+20=0
t2-7t+20=0
Δx=72-4×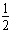 ×20=9有解,能追上
×20=9有解,能追上
且t1=4,t2=10(舍去)
∴在t=4s末追上车
x人=vt
x车=x0+
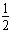 at2
at2 要追上汽车,则要求Δx=x车-x人=0
(1)当v=6m/s代入上式可得
Δx=
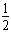 t2-6t+20=0
t2-6t+20=0 ∵Δx=62-4×
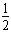 ×20<0
×20<0 ∴Δx不能为零,不能追上
且Δx=
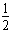 (t-6)2+2
(t-6)2+2 当t=6s时,Δx最小为2m
(2)当v=7m/s代入上式
Δx=
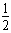 t2-7t+20=0
t2-7t+20=0 Δx=72-4×
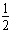 ×20=9有解,能追上
×20=9有解,能追上且t1=4,t2=10(舍去)
∴在t=4s末追上车

练习册系列答案
相关题目
