题目内容
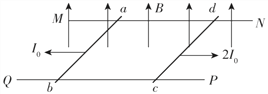
【题目】如图所示，无限长平行金属导轨EF、PQ固定在倾角θ=37°的光滑绝缘斜面上，轨道间距L=1m，底部接入一阻值R=0.06Ω的定值电阻，上端开口，垂直斜面向上的匀强磁场的磁感应强度B=2T。一质量m=2kg的金属棒ab与导轨接触良好，ab与导轨间的动摩擦因数μ=0.5，ab连入导轨间的电阻r=0.04Ω，电路中其余电阻不计。现用一质量M=6kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放物体，当物体下落高度h=2.0m时，ab开始匀速运动，运动中ab始终垂直导轨并与导轨接触良好。不计空气阻力，sin37°=0.6，cos37°=0.8，g取10m/s2。
(1)求ab棒沿斜面向上运动的最大速度；
(2)在ab棒从开始运动到开始匀速运动的这段时间内，求通过杆的电量q；
(3)在ab棒从开始运动到开始匀速运动的这段时间内，求电阻R上产生的焦耳热。
【答案】(1)
(2)q=40C (3)
【解析】
(1)由静止释放物体，ab棒先向上做加速运动，随着速度增大，产生的感应电流增大，棒所受的安培力增大，加速度减小，棒做加速度减小的加速运动；当加速度为零时，棒开始匀速，速度达到最大。据法拉第电磁感应定律、闭合电路的欧姆定律、安培力公式、平衡条件等知识可求出棒的最大速度。
(2)本小问是感应电量的问题，据法拉第电磁感应定律、闭合电路的欧姆定律、电流的定义式、磁通量的概念等知识可进行求解。
(3)从ab棒开始运动到匀速运动，系统的重力势能减小，转化为系统增加的动能、摩擦热和焦耳热，据能量守恒定律可求出系统的焦耳热，再由焦耳定律求出电阻R上产生的焦耳热。
(1)金属棒ab和物体匀速运动时，速度达到最大值，由平衡条件知
对物体，有
；对ab棒，有
又
、
联立解得：
(2) 感应电荷量
据闭合电路的欧姆定律
据法拉第电磁感应定律
在ab棒开始运动到匀速运动的这段时间内，回路中的磁通量变化
联立解得：
(3)对物体和ab棒组成的系统，根据能量守恒定律有：
又
解得：电阻R上产生的焦耳热
