题目内容
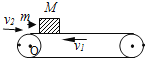
【题目】如图所示,质量M=1.0kg的木块随足够长的传送带一起以v1=2.0m/s的速度向左匀速运动,木块与传送带间的动摩擦因数μ=0.50,当木块运动到转轴O点时,一颗质量m=20g的子弹以v2=300m/s的速度水平向右击穿木块,穿出时子弹的速度v2’=50m/s.设传送带速度恒定,子弹与木块作用时间极短,木块的质量不变,g=10m/s2,求:
(1)子弹击穿木块时,木块速度的大小和方向.
(2)子弹击穿木块过程中,子弹和木块组成的系统损失的机械能.
(3)被子弹击穿后,木块向右运动距O点的水平最大距离.
【答案】(1)3m/s,方向向右;(2)872.5J(3)0.90m
【解析】
(1)设向右为正方向,木块被子弹击穿时的速度为u,子弹击穿木块过程动量守恒,故:
mv0-Mv=mv1+Mu
代入数据解得:u=3.0m/s
(2)子弹击穿木块过程中,子弹和木块组成的系统损失的机械能:E=![]() mv02+
mv02+![]() Mv2-
Mv2-![]() mv12-
mv12-![]() Mu2
Mu2
代入数据解得:E=872.5J
(3)设子弹穿出木块后,木块向右做匀减速运动的加速度为a,根据牛顿第二定律有:μmg=ma
代入数据得:a=5.0m/s2
木块向右运动到离A点最远时,速度为零,设木块向右移动最大距离为s1,有:
u2=2as1
代入数据解得:s1=0.90m
故本题答案是:(1)3m/s,方向向右;(2)872.5J(3)0.90m

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为0.10s。
(1)试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F 5个点时小车的瞬时速度,并将各个速度值填入表中。(要求保留三位有效数字)
![]()
vB | vC | vD | vE | vF | |
数值/(m·s-1) | ___ | ___ | ___ | ___ | ___ |
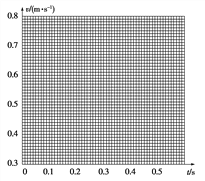
(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并在图中画出小车的瞬时速度随时间变化的关系图线________。