题目内容
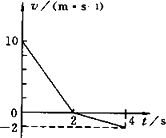
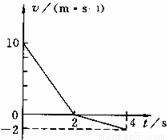
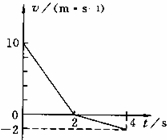在粗糙水平面上质量为m=20kg的物体，沿水平面做直线运动．运动过程受到大小恒定的力F作用，（0～2s）内F与运动方向相反，（2～4s）内F与运动方向相同，物体的速度与时间的关系图象如图，g取10m/s2．求物体与水平面间的动摩擦因数．
解：由斜率等于加速度的大小，得到：前2s内和后2s内物体的加速度大小分别为
a1=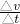
=|
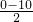|=5m/s2，a2=|
|=1 m/s2
根据牛顿第二定律得
（0～2s）内 F+f=ma1
（2～4s）内 F-f=ma2
又 f=?N=?mg
求得 ?=0.2
答：物体与水平面间的动摩擦因数为0.2．
分析：由速度图象的斜率求出加速度，分析求出前2s内和后2s内物体的加速度大小，再根据牛顿第二定律求出拉力F和摩擦力的大小．
点评：本题速度图象反映了物体的运动情况，抓住斜率等于加速度，结合牛顿第二定律进行求解，基础题．
a1=
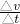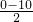=||=5m/s2，a2=||=1 m/s2 根据牛顿第二定律得
（0～2s）内 F+f=ma1
（2～4s）内 F-f=ma2
又 f=?N=?mg
求得 ?=0.2
答：物体与水平面间的动摩擦因数为0.2．
分析：由速度图象的斜率求出加速度，分析求出前2s内和后2s内物体的加速度大小，再根据牛顿第二定律求出拉力F和摩擦力的大小．
点评：本题速度图象反映了物体的运动情况，抓住斜率等于加速度，结合牛顿第二定律进行求解，基础题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
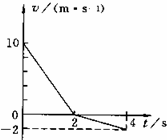在粗糙水平面上质量为m=20kg的物体，沿水平面做直线运动．运动过程受到大小恒定的力F作用，（0～2s）内F与运动方向相反，（2～4s）内F与运动方向相同，物体的速度与时间的关系图象如图，g取10m/s2．求物体与水平面间的动摩擦因数．
