题目内容
滑板运动是一项陆地上的“冲浪运动”滑板运动员可在不同的滑坡上滑行,做出各种动作,给人以美的享受.如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37,de段是一半径R=2.5m的四分之一圆弧轨道,0点为圆心,其正上方的d点为圆弧的最高点.滑板及运动员的总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示.忽略摩擦阻力和空气阻力,取g=10m/s2,sin 37°=0.6,eos 37°=0.8.除下述问题(3)中运动员做缓冲动作以外,均可把滑板及运动员视为质点.(1)若运动员从bc 段紧靠b处无初速度滑下,求Nd的大小.
(2)运动员逐渐减小从bc上无初速度下滑时距水平地面的高度h,请在图乙的坐标系中作出Nd-h图象(只根据作出的图象评分,不要求写出计算过程和作图依据).
(3)运动员改为从b点以v=4m/s的速度水平滑出,落在bc上时通过短暂的缓冲动作使他沿斜面方向继续滑行,则他是否会从d点滑离轨道?请通过计算得出结论.

【答案】分析:(1)运动员从开始滑下至滑到d点,由机械能守恒定律求出d点速度,根据牛顿第二定律求出轨道对滑板支持力.
(2)根据Nd-h的关系式作图.
(3)运动员离开b点做平抛运动,落在斜面上时,竖直方向上的位移和水平方向上的位移的比值等于tanθ,根据这一关系求出运动的时间,从而求出落在斜面上时在竖直方向上的分速度.落在bc上时通过短暂的缓冲动作使他只保留沿斜面方向的速度继续滑行,对落地点的速度沿垂直斜面方向和沿斜面方向正交分解,求出沿斜面方向的分速度,即为沿斜面滑行的速度,然后根据动能定理求出d点的速度,与d点的临界速度进行比较,判断是否会从d点滑离轨道.
解答: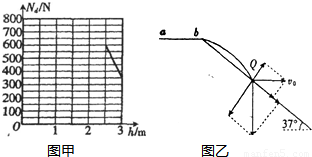 解:(1)运动员从开始滑下至滑到d点,由机械能守恒定律得:
解:(1)运动员从开始滑下至滑到d点,由机械能守恒定律得:
mg(H-R)= mv2
mv2
在d点,根据牛顿第二定律得:
mg-Nd=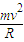
解得:Nd=mg(1-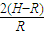 )=360N
)=360N
(2)根据Nd=mg(1-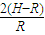 )作出Nd-h图象如图甲所示.
)作出Nd-h图象如图甲所示.
(3)当以v=4m/s的速度从b点水平滑出时,运动员做平抛落在Q点,如图乙所示,
设bQ=x,则有
xsin37°= gt2
gt2
xcos37°=vt
解得:t=0.6 S
vy=gt=6m/s
在Q点缓冲后,在Q的速度
从Q→d根据机械静守恒定律,有:
mg(H- gt2)-mgR=
gt2)-mgR= mvd2-
mvd2- mvQ2
mvQ2
运动员恰从d点滑离轨道应满足mg=m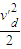
解得: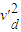 -
-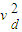 =4.76 即 vd<vd′
=4.76 即 vd<vd′
可见滑板运动员不会从圆弧最高点d滑离轨道.
答:(1)若运动员从bc 段紧靠b处无初速度滑下,Nd的大小是360N.
(2)如上图
(3)滑板运动员不会从圆弧最高点d滑离轨道.
点评:解决本题的关键知道平抛运动落在斜面上,竖直方向上的位移和水平方向上的位移的比值是定值,根据该关系可求出时间.以及在外轨道做圆周运动,最高点有最大速度,此时正压力为0,有mg=m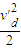 .
.
(2)根据Nd-h的关系式作图.
(3)运动员离开b点做平抛运动,落在斜面上时,竖直方向上的位移和水平方向上的位移的比值等于tanθ,根据这一关系求出运动的时间,从而求出落在斜面上时在竖直方向上的分速度.落在bc上时通过短暂的缓冲动作使他只保留沿斜面方向的速度继续滑行,对落地点的速度沿垂直斜面方向和沿斜面方向正交分解,求出沿斜面方向的分速度,即为沿斜面滑行的速度,然后根据动能定理求出d点的速度,与d点的临界速度进行比较,判断是否会从d点滑离轨道.
解答:
 解:(1)运动员从开始滑下至滑到d点,由机械能守恒定律得:
解:(1)运动员从开始滑下至滑到d点,由机械能守恒定律得:mg(H-R)=
 mv2
mv2在d点,根据牛顿第二定律得:
mg-Nd=
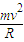
解得:Nd=mg(1-
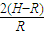 )=360N
)=360N(2)根据Nd=mg(1-
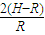 )作出Nd-h图象如图甲所示.
)作出Nd-h图象如图甲所示.(3)当以v=4m/s的速度从b点水平滑出时,运动员做平抛落在Q点,如图乙所示,
设bQ=x,则有
xsin37°=
 gt2
gt2xcos37°=vt
解得:t=0.6 S
vy=gt=6m/s
在Q点缓冲后,在Q的速度
从Q→d根据机械静守恒定律,有:
mg(H-
 gt2)-mgR=
gt2)-mgR= mvd2-
mvd2- mvQ2
mvQ2运动员恰从d点滑离轨道应满足mg=m
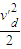
解得:
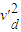 -
-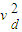 =4.76 即 vd<vd′
=4.76 即 vd<vd′可见滑板运动员不会从圆弧最高点d滑离轨道.
答:(1)若运动员从bc 段紧靠b处无初速度滑下,Nd的大小是360N.
(2)如上图
(3)滑板运动员不会从圆弧最高点d滑离轨道.
点评:解决本题的关键知道平抛运动落在斜面上,竖直方向上的位移和水平方向上的位移的比值是定值,根据该关系可求出时间.以及在外轨道做圆周运动,最高点有最大速度,此时正压力为0,有mg=m
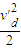 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2008?福建模拟)滑板运动是一项陆地上的“冲浪运动”滑板运动员可在不同的滑坡上滑行,做出各种动作,给人以美的享受.如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=370,de段是一半径R=2.5m的四分之一圆弧轨道,0点为圆心,其正上方的d点为圆弧的最高点.滑板及运动员的总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示.忽略摩擦阻力和空气阻力,取g=10m/s2,sin 37°=0.6,eos 37°=0.8.除下述问题(3)中运动员做缓冲动作以外,均可把滑板及运动员视为质点.
(2008?福建模拟)滑板运动是一项陆地上的“冲浪运动”滑板运动员可在不同的滑坡上滑行,做出各种动作,给人以美的享受.如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=370,de段是一半径R=2.5m的四分之一圆弧轨道,0点为圆心,其正上方的d点为圆弧的最高点.滑板及运动员的总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示.忽略摩擦阻力和空气阻力,取g=10m/s2,sin 37°=0.6,eos 37°=0.8.除下述问题(3)中运动员做缓冲动作以外,均可把滑板及运动员视为质点. 滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性.如图所示,abcdef为同一竖直平面内的滑行轨道,其中bc段水平,ab、de和ef段均为倾角θ=37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略).已知H1=5m,L=15m,H2=1.25m,H3=12.75m,设滑板与轨道之间的摩擦力为它们间压力的k倍(k=0.25),运动员连同滑板的总质量m=60kg.运动员从a点由静止开始下滑从c点水平飞出,在de上着陆后,经短暂的缓冲动作后保留沿斜面方向的分速度下滑,接着在def轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性.如图所示,abcdef为同一竖直平面内的滑行轨道,其中bc段水平,ab、de和ef段均为倾角θ=37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略).已知H1=5m,L=15m,H2=1.25m,H3=12.75m,设滑板与轨道之间的摩擦力为它们间压力的k倍(k=0.25),运动员连同滑板的总质量m=60kg.运动员从a点由静止开始下滑从c点水平飞出,在de上着陆后,经短暂的缓冲动作后保留沿斜面方向的分速度下滑,接着在def轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.求: 滑板运动是一项陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作给人以美的享受.如图所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37°,bc段与和cd段之间由长度不计的小圆弧衔接,滑板及运动员在转弯处c无机械能损失.de段是一半径R=2.5m的四分之一圆弧轨道,O点为圆心,其正上方的d点为圆弧的最高点,滑板及运动员总质量m=60kg,忽略摩擦阻力和空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.运动员从b点以υ0=4m/s的速度水平滑出,落在bc上时通过短暂的缓冲动作使他只保留沿斜面方向的速度继续滑行,除运动员做缓冲动作以外,均可把滑板及运动员视为质点.则他是否会从d点滑离轨道?请通过计算得出结论.
滑板运动是一项陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作给人以美的享受.如图所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37°,bc段与和cd段之间由长度不计的小圆弧衔接,滑板及运动员在转弯处c无机械能损失.de段是一半径R=2.5m的四分之一圆弧轨道,O点为圆心,其正上方的d点为圆弧的最高点,滑板及运动员总质量m=60kg,忽略摩擦阻力和空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.运动员从b点以υ0=4m/s的速度水平滑出,落在bc上时通过短暂的缓冲动作使他只保留沿斜面方向的速度继续滑行,除运动员做缓冲动作以外,均可把滑板及运动员视为质点.则他是否会从d点滑离轨道?请通过计算得出结论. 滑板运动是一项陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作给人以美的享受.如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37°,de段是一半径R=2.5m的四分之一圆弧轨道,O点为圆心,其正上方的d点为圆弧的最高点,滑板及运动员总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示,忽略摩擦阻力和空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.除下述问(2)中运动员做缓冲动作以外,均可把滑板及运动员视为质点.
滑板运动是一项陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作给人以美的享受.如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37°,de段是一半径R=2.5m的四分之一圆弧轨道,O点为圆心,其正上方的d点为圆弧的最高点,滑板及运动员总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示,忽略摩擦阻力和空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.除下述问(2)中运动员做缓冲动作以外,均可把滑板及运动员视为质点.