��Ŀ����
13��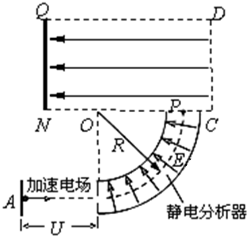 ��ͼ��ʾ����ֹ��A�������ӣ�����ѹΪU�ļ��ٵ糡���ٺ���ͼ��Բ������ͨ������������������ھ������������Բ���˶�����P�㴹ֱCN��������������ǿ�糡���糡����ˮƽ��������ǡ�ܴ���Q�㣮���������ͨ���ǰ뾶ΪR��$\frac{1}{4}$Բ�������о��ȷ���ֲ��ĵ糡��������ͼ��ʾ����������Ϊm�������Ϊq��QN=d��PN=2d�������������ƣ���
��ͼ��ʾ����ֹ��A�������ӣ�����ѹΪU�ļ��ٵ糡���ٺ���ͼ��Բ������ͨ������������������ھ������������Բ���˶�����P�㴹ֱCN��������������ǿ�糡���糡����ˮƽ��������ǡ�ܴ���Q�㣮���������ͨ���ǰ뾶ΪR��$\frac{1}{4}$Բ�������о��ȷ���ֲ��ĵ糡��������ͼ��ʾ����������Ϊm�������Ϊq��QN=d��PN=2d�������������ƣ�����1�����ӵĵ��ԣ�
��2������������������˶��켣���糡ǿ��E�Ĵ�С��
��3��P��Q�����ĵ�ѹU1��
���� ��1�����������ھ�����������˶��жϵ���
��2���ڼ��ٵ糡���ɶ��ܶ�������ٶȣ��ھ���������е糡���ṩ������
��3����ƫת�糡����������ƽ���˶���������ֱ�������٣�ˮƽ�����ȼ��ټ������
��� �⣺��1�������ھ������������Բ���˶������ݵ糡���ṩ��Բ���˶�����������֪�����Ӵ����磻
��2���ڼ��ٵ糡�У��ɶ��ܶ����ɵã�$qU=\frac{1}{2}m{v}^{2}$
�ھ�����������У�qE=$\frac{m{v}^{2}}{R}$
������ã�E=$\frac{2U}{R}$
��3������ƫת�糡����ֱ���������˶���ˮƽ�����ȼ����˶���
d=vt
2d=$\frac{1}{2}•\frac{q{U}_{1}}{2md}{t}^{2}$
������ã�U1=16U
�𣺣�1�����Ӵ�����
��2������������������˶��켣���糡ǿ��E�Ĵ�СΪ$\frac{2U}{R}$
��3��P��Q�����ĵ�ѹU1Ϊ16U
���� ���ڴ��������ڵ糡�м��ٹ��̣��������ö��ܶ����о����ٵ�ѹ���ٶȵĹ�ϵ�����ڵ糡��ƫת���⣬�˶��ķֽ��dz��÷�����

��ϰ��ϵ�д�
�����Ŀ
3��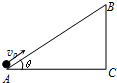 ��ͼ��ʾ����ΪL����бΪ�ȵĹ⻬��Եб�洦�ڵ糡�У�һ������Ϊ+q������Ϊm ��С���Գ��ٶ�vO��б��˵�A �㿪ʼ��б���ϻ�������б�涥�˵��ٶ���ΪvO��������
��ͼ��ʾ����ΪL����бΪ�ȵĹ⻬��Եб�洦�ڵ糡�У�һ������Ϊ+q������Ϊm ��С���Գ��ٶ�vO��б��˵�A �㿪ʼ��б���ϻ�������б�涥�˵��ٶ���ΪvO��������
 ��ͼ��ʾ����ΪL����бΪ�ȵĹ⻬��Եб�洦�ڵ糡�У�һ������Ϊ+q������Ϊm ��С���Գ��ٶ�vO��б��˵�A �㿪ʼ��б���ϻ�������б�涥�˵��ٶ���ΪvO��������
��ͼ��ʾ����ΪL����бΪ�ȵĹ⻬��Եб�洦�ڵ糡�У�һ������Ϊ+q������Ϊm ��С���Գ��ٶ�vO��б��˵�A �㿪ʼ��б���ϻ�������б�涥�˵��ٶ���ΪvO��������| A�� | С����B ��ĵ�����һ������С����A ��ĵ����� | |
| B�� | A��B����ĵ��Ʋ�һ��Ϊ $\frac{mgL}{q}$ | |
| C�� | ���糡����ǿ�糡����õ糡�ij�ǿ����Сֵһ���� $\frac{mgsin��}{q}$ | |
| D�� | �˶�������С������������糡������� |
8����ͼ��ʾ��һϸ������Ϊm����ʼʱ��=30�㣬����ľ���Ժ㶨�ٶ��������˶�����ϸ���ܵ�ľ�������������
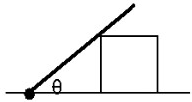

| A�� | һֱ���� | B�� | һֱ��С | C�� | ��������С | D�� | �ȼ�С������ |
18������������������ܴ�������������뾶��С�������ٶȺ����ڱ仯����ǣ�������
| A�� | �ٶȼ�С�����������ܼ�С | B�� | �ٶȼ�С�����ڼ�С�����ܼ�С | ||
| C�� | �ٶ������������������� | D�� | �ٶ��������ڼ�С���������� |
3��һ����������˶�������ƣ��������˶�һ��ҹ��ʱ��Ϊa�룮��ͬһ���ɲ����Ʋ�ij�����������ڳ�����Ķ�������������b����bС��1����������������ΪG��������ǵ�ƽ���ܶ�Ϊ��������
| A�� | $\frac{30��}{{G{a^2}b}}$ | B�� | $\frac{3��}{{G{a^2}{b^2}}}$ | C�� | $\frac{30��}{{G{a^2}{{��1-b��}^2}}}$ | D�� | $\frac{3��}{{G{a^2}{{��1-b��}^{\;}}}}$ |
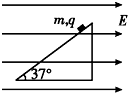 ��ͼ��ʾ���⻬б�����Ϊ37�㣬һ���������С�������Ϊm�������Ϊq������б���ϣ�����ˮƽ�������ͼ��ʾ����ǿ�糡ʱ������С���ǡ�þ�ֹ��б���ϣ���ijʱ�̿�ʼ���糡ǿ�ȱ�Ϊԭ����$\frac{1}{3}$����
��ͼ��ʾ���⻬б�����Ϊ37�㣬һ���������С�������Ϊm�������Ϊq������б���ϣ�����ˮƽ�������ͼ��ʾ����ǿ�糡ʱ������С���ǡ�þ�ֹ��б���ϣ���ijʱ�̿�ʼ���糡ǿ�ȱ�Ϊԭ����$\frac{1}{3}$����


 ���ػ���ֱ����һ���������ٶ���ʱ��Ĺ�ϵ��ͼ��ʾ��
���ػ���ֱ����һ���������ٶ���ʱ��Ĺ�ϵ��ͼ��ʾ��