题目内容
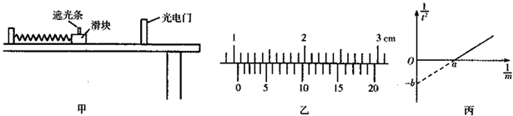
18.为了探究加速度与力、质量的关系,甲、乙、丙三位同学分别设计了如图所示实验装置,小车总质量用M表示(乙图中M包括小车与传感器,丙图中M包括小车和与小车固连的滑轮),钩码总质量用m表示.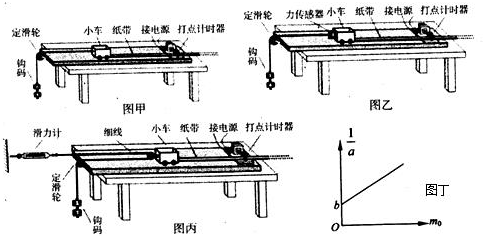
(1)三组实验中需要平衡小车与长木板间摩擦力甲乙丙;(用甲、乙、丙表示)
(2)三组实验中需满足M>>m的是甲;
(3)若采用图甲所示的方法研究“在外力一定的条件下,物体的加速度与其质量的关系”,M为小车总质量,(其中小车自身质量用M0表示,车上所加砝码质量用m0表示)所画出的实验图象如图丁所示.设图中直线的斜率为k,在纵轴上的截距为b,则小车受到的拉力为F=$\frac{1}{k}$,小车的质量为M0=$\frac{b}{k}$.
分析 (1、2)根据实验原理,即可判定是否需要平衡摩擦力,及确定所挂钩码的总质量m与小车的总质量M的关系;
(3)根据牛顿第二定律写出$\frac{1}{a}$与小车上砝码质量m0的表达式,然后结合斜率与截距概念求解即可.
解答 解:(1)三组实验都是用绳子的拉力表示小车受到的合外力,所以都需要平静摩擦力;
(2)甲图通过钩码的总质量对应的重力代替绳子的拉力合外力,乙图中小车受到的合外力是力传感器的示数,丙图小车受到的合外力则是测力计的2倍,因此三组实验中只有甲需要满足所挂钩码的总质量m远小于小车的总质量M的条件;
(3)根据牛顿第二定律得:F=(M0+m0)a,
变形得$\frac{1}{a}=\frac{1}{F}{m}_{0}+\frac{{M}_{0}}{F}$
所以$\frac{1}{a}-{m}_{0}$图线的斜率表示$\frac{1}{F}$,
则k=$\frac{1}{F}$,解得F=$\frac{1}{k}$;
纵轴截距$\frac{{M}_{0}}{F}$=b,解得小车质量M0=$\frac{b}{k}$.
故答案为:(1)甲乙丙;(2)甲;(3)$\frac{1}{k}$;$\frac{b}{k}$
点评 考查不同实验中,是否平衡摩擦力,是依据实验原理,并不是统统平衡的,并掌握牛顿第二定律的应用,注意力传感器的作用,及理解测力计的读数与小车的合力的关系,是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
3.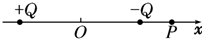 如图所示,在x轴上关于原点O对称的两点固定放置等量异种点电荷+Q和-Q,x轴上的P点位于-Q的右侧.下列判断正确的是( )
如图所示,在x轴上关于原点O对称的两点固定放置等量异种点电荷+Q和-Q,x轴上的P点位于-Q的右侧.下列判断正确的是( )
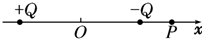 如图所示,在x轴上关于原点O对称的两点固定放置等量异种点电荷+Q和-Q,x轴上的P点位于-Q的右侧.下列判断正确的是( )
如图所示,在x轴上关于原点O对称的两点固定放置等量异种点电荷+Q和-Q,x轴上的P点位于-Q的右侧.下列判断正确的是( )| A. | 在x轴上还有一点与P点电场强度相同 | |
| B. | 在x轴上还有两点与P点电场强度相同 | |
| C. | 若将一试探电荷+q从P点沿x轴移至O点,电势能先减小后增大 | |
| D. | 若将一试探电荷+q从P点沿x轴移至O点,电势能减小 |
7. 有一个带负电的粒子,从一条电场线上的A点以某一初速度射出,仅在电场力作用下沿该电场线运动到B点,其电势能EP随位移x变化的关系如图所示,则下列说法正确的是( )
有一个带负电的粒子,从一条电场线上的A点以某一初速度射出,仅在电场力作用下沿该电场线运动到B点,其电势能EP随位移x变化的关系如图所示,则下列说法正确的是( )
 有一个带负电的粒子,从一条电场线上的A点以某一初速度射出,仅在电场力作用下沿该电场线运动到B点,其电势能EP随位移x变化的关系如图所示,则下列说法正确的是( )
有一个带负电的粒子,从一条电场线上的A点以某一初速度射出,仅在电场力作用下沿该电场线运动到B点,其电势能EP随位移x变化的关系如图所示,则下列说法正确的是( )| A. | 该电场不可能是匀强电场 | B. | 粒子运动的速度越来越大 | ||
| C. | 粒子运动的加速度越来越大 | D. | 粒子运动的轨迹为曲线 |
8.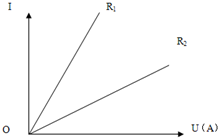 现有电阻R1、R2,它们的电流和电压间关系表示在图中,当它们两端电压相等时,电阻R1和R2所消耗的功率分别为P1、P2,则可知( )
现有电阻R1、R2,它们的电流和电压间关系表示在图中,当它们两端电压相等时,电阻R1和R2所消耗的功率分别为P1、P2,则可知( )
 现有电阻R1、R2,它们的电流和电压间关系表示在图中,当它们两端电压相等时,电阻R1和R2所消耗的功率分别为P1、P2,则可知( )
现有电阻R1、R2,它们的电流和电压间关系表示在图中,当它们两端电压相等时,电阻R1和R2所消耗的功率分别为P1、P2,则可知( )| A. | R1>R2,P1>P2 | B. | R1>R2,P1<P2 | C. | R1<R2,P1>P2 | D. | R1<R2,P1<P2 |

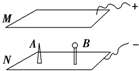 如图所示,金属板M接高压电源的正极,金属板N接负极.金属板N上有两个等高的金属柱A、B,其中A为尖头,B为圆头.逐渐升高电源电压,当电压达到一定值时,可看到放电现象.先产生放电现象的是A,这种放电现象叫做尖端放电.
如图所示,金属板M接高压电源的正极,金属板N接负极.金属板N上有两个等高的金属柱A、B,其中A为尖头,B为圆头.逐渐升高电源电压,当电压达到一定值时,可看到放电现象.先产生放电现象的是A,这种放电现象叫做尖端放电.