题目内容
10.闭合线圈与匀强磁场垂直,现将线圈拉出磁场,第一次拉出速度为v1,第二次拉出速度为v2,且v2=2v1,则( )| A. | 两次拉力做的功一样多 | B. | 两次所需拉力一样大 | ||
| C. | 两次拉力的功率一样大 | D. | 两次通过线圈的电荷量一样多 |
分析 在恒力作用下,矩形线圈被匀速拉出时,拉力与安培力大小相等,拉力做功等于拉力与位移的乘积,而拉力功率等于拉力与速度的乘积,线圈产生的焦耳热等于拉力做的功.根据E=BLv、I=$\frac{E}{R}$和F=BIL推导出安培力与速度的关系$\frac{{B}^{2}{L}^{2}v}{R}$,再列出拉力、功率和电荷量的表达式,再运用比例法求解.
解答 解:A、B、线框的速度为v1时,产生的感应电流为:I=$\frac{B{L}_{1}{v}_{1}}{R}$
线框所受的安培力大小为:FA1=BIL1=$\frac{{B}^{2}{L}_{1}^{2}{v}_{1}}{R}$,
由于线框匀速运动,则拉力为:F1=FA1=$\frac{{B}^{2}{L}_{1}^{2}{v}_{1}}{R}$,拉力做的功为:W1=F1L2=$\frac{{B}^{2}{L}_{1}^{2}{v}_{1}}{R}$L2
同理,线框的速度为v2,时,拉力为:F2=FA2=$\frac{{B}^{2}{L}_{1}^{2}{v}_{2}}{R}$,拉力做的功为:W2=F2L2=$\frac{{B}^{2}{L}_{1}^{2}{v}_{2}}{R}$L2
因为v2=2v1,则2F1=F2,2W1=W2,可见速度越大,所用的拉力越大,拉力做功越大.则第二次拉力和拉力做功较大,故A、B错误.
C、拉力的功率 P=Fv=$\frac{{B}^{2}{L}_{1}^{2}v}{R}$•v∝v2,所以第二次拉力的功率大,故C错误.
D、两种情况下,线框拉出磁场时穿过线框的磁通量的变化量相等,根据感应电荷量公式q=$\frac{△∅}{R}$可知,通过导线截面的电量相等.故D正确.
故选:D.
点评 本题的关键要掌握安培力的推导方法和感应电荷量的表达式.要对两种情况下物理量进行比较,我们应该先把要比较的物理量表示出来再解题.

 如图所示,水平地面上有两块完全相同的木块A、B,在水平推力F的作用下运动,用FAB代表A、B间的相互作用力,则( )
如图所示,水平地面上有两块完全相同的木块A、B,在水平推力F的作用下运动,用FAB代表A、B间的相互作用力,则( )| A. | 若地面是完全光滑的,FAB=F | B. | 若地面是有摩擦的,FAB=F | ||
| C. | 若地面是完全光滑的,FAB=$\frac{F}{2}$ | D. | 若地面是有摩擦的,FAB=2F |
| A. | $\frac{d{V}_{1}}{{V}_{2}}$ | B. | $\frac{d{V}_{2}}{{V}_{1}}$ | C. | $\frac{d{V}_{2}}{\sqrt{{{V}_{2}}^{2}-{{V}_{1}}^{2}}}$ | D. | $\frac{d\sqrt{{{V}_{1}}^{2}+{{V}_{2}}^{2}}}{{V}_{2}}$ |
 如图,为由两个振动情况完全相同的振源发出的两列波在空间相遇而叠加所产生的图样,每列波振幅均为A,其中实线表示波峰,虚线表示波谷,则关于介质中的a、b、c、d四点,(b、c为相邻波峰和波谷的中点)下列说法正确的是( )
如图,为由两个振动情况完全相同的振源发出的两列波在空间相遇而叠加所产生的图样,每列波振幅均为A,其中实线表示波峰,虚线表示波谷,则关于介质中的a、b、c、d四点,(b、c为相邻波峰和波谷的中点)下列说法正确的是( )| A. | a、c振幅为2A,b、d始终不动 | |
| B. | 图示时刻d点位移大小为2A,b、c、d三点位移为零 | |
| C. | a点位移大小始终为2A,d点位移始终为零 | |
| D. | 这四个点全部是振动减弱点 |
 如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )
如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )| A. | 该波的传播速率为4 m/s | |
| B. | 该波的传播方向沿x轴正方向 | |
| C. | 经过0.5 s时间,质点P沿波的传播方向向前传播2 m | |
| D. | 该波在传播过程中若遇到8 m的障碍物,能发生明显衍射现象 |
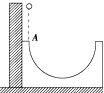 如图所示,将一个内外侧均光滑的半圆形槽置于光滑的水平面上,槽的左侧有一竖直墙壁.现让一小球自左端槽口A点的正上方由静止开始下落,从A点与半圆形槽相切进入槽内,不计空气阻力,下列说法正确的是( )
如图所示,将一个内外侧均光滑的半圆形槽置于光滑的水平面上,槽的左侧有一竖直墙壁.现让一小球自左端槽口A点的正上方由静止开始下落,从A点与半圆形槽相切进入槽内,不计空气阻力,下列说法正确的是( )| A. | 小球从开始下落至运动到半圆形槽最低点的过程中,重力的功率越来越大 | |
| B. | 小球从开始下落到从右侧离开槽的过程中,小球的机械能守恒 | |
| C. | 小球从右侧离开半圆形槽后,能上升到与开始下落位置高度相同的地方 | |
| D. | 小球从刚进入半圆形槽到从右侧离开槽的过程中,小球与槽组成的系统机械能守恒 |
 油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.6mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的纯油膜的形状如图所示.若每一个小方格的边长为25mm,试问:
油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.6mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的纯油膜的形状如图所示.若每一个小方格的边长为25mm,试问: 如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求:
如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定有一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求: